Множество вещественных чисел

Понятие множество является одним из основных в математике. Оно принадлежит к так называемым первичным, неопределяемым понятиям.

Слова «совокупность», «семейство», «набор» и т.п. − синонимы слова «множество».

Множество может содержать конечное или бесконечное число произвольных объектов. Объекты, из которых состоит множество, называют его элементами или точками. Множества часто обозначают большими буквами, а их элементы − малыми.

или

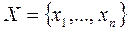− множество Х состоит из элементов …

X и Y − два множества. X=Y, если они состоят из одних и тех же элементов.

Если в Х нет элементов, не принадлежащих Y, то говорят, Х − подмножество множества Y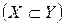

В математике часто используется пустое множество. Оно не содержит ни одного элемента. Æ

Некоторые логические символы: $ − существует, " − любой.

Из курса элементарной математики известно, что множество вещественных чисел состоит из рациональных и иррациональных чисел. Рациональным называется число, которое можно представить в виде p/q, где p и q − целые числа, причем q¹0. Всякое рациональное число является либо целым, либо представляется конечной или бесконечной периодической дробью.

Иррациональное число представляется непериодической бесконечной десятичной дробью.

Вещественные числа можно изобразить точками координатной прямой.

Пусть a<b − два числа. Будем пользоваться следующими обозначениями

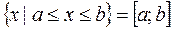
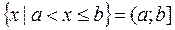; [a;b); (a;b)

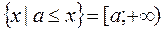(a; +¥) (-¥;b) (-¥;b] (-¥;+¥)

Все эти множества называются промежутками, причем [a;b] − отрезок, [a;b), (a;b], (-¥;b], [a; +¥) − полуинтервалы, а (a;b), (a; +¥), (-¥;b), (-¥;+¥) − интервалы.

Промежутки [a;b), (a;b], (a;b) и [a;b] называются конечными, остальные − бесконечные.

Абсолютной величиной (или модулем) числа х называется само число х, если х³0, число –х, если x<0.

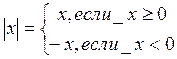
Из определения вытекает ряд свойств:

1)

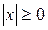
2) |x|=|-x|

3) -|x|£x£|x|

4) Пусть e − положительное число. |x|£e и -e£ x £e − равносильны

5)

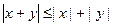
6)

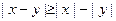
7) и , если y¹0.