Геодезическая линия и локсодромия

Геодезической линией называется кратчайшая кривая между двумя точками на земной сфероиде. Одно из свойств этой кривой состоит в том, что любой ее элементарный отрезок находится в плоскости, перпендикулярной к поверхности сфероида. В то же время на большом протяжении геодезическая линия не лежит в одной плоскости, за исключением тех частных случаев, когда она совпадает с меридианом или экватором. Таким образом, геодезическая линия является пространственной, а не плоской кривой или, иначе говоря, кривой двоякой кривизны. Наглядным аналогом геодезической линии может служить нить, туго натянутая между двумя точками поверхности сфероида.

В курсе сферической геодезии показано, что геодезическая линия описывается следующей системой дифференциальных уравнений:

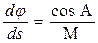; (2.16)

; (2.17)

, (2.18)

где s – длина геодезической линии, а ds – ее элементарный отрезок;

А – азимут, определяемый как угол между северной частью меридиана и направлением геодезической линии в точке с координатами φ, λ.

С использованием этих уравнений можно найти координаты точек, принадлежащих одной геодезической линии, или определить минимальное расстояние между заданными точками на сфероиде и направление кратчайшей линии из одной точки в другую. Правда, прямому интегрированию эти уравнения не поддаются, а возможны лишь приближенные (с любой степенью точности) численные решения.

Как видно из уравнения (2.18), направление геодезической линии в общем случае является переменным. Поэтому для движения судна в пункт назначения по кратчайшему пути необходимо непрерывно изменять курс, что представляет определенные трудности. На практике судно всегда следует в течение более или менее продолжительных интервалов времени постоянными курсами.

Линия, пересекающая все меридианы под одинаковыми углами, называется локсодромией. Она описывается системой дифференциальных уравнений (2.16) и (24) совместно с уравнением dA / ds = 0 или A = const. При этом под ds подразумевается элементарный отрезок локсодромии.

В отличие от уравнений геодезической линии, система дифференциальных уравнений локсодромии поддается точному интегрированию и позволяет получить явную зависимость между координатами точек локсодромии и ее направлением.

На основании уравнений (2.16) и (2.17) можно записать соотношение

,

откуда

.

Проинтегрируем это уравнение в пределах широт φ₀ ÷ φ₁ и соответствующих им долгот λ₀ ÷ λ₁ :

. (2.19)

Главные радиусы кривизны земного сфероида M и N зависят от широты φ. Их отношение также является функцией широты:

.

Учитывая, что , получим

.

После подстановки этого выражения в уравнение (2.19) интеграл в правой его части будет представлен как разность двух интегралов, имеющих простое решение

.

Первый интеграл является табличным

.

Второй интеграл решается с помощью замены переменной

Для обратного перехода от ψ до φ воспользуемся известным тригонометрическим тождеством

,

принимая в нашем случае ; .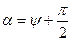

Тогда

.

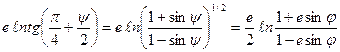Переходя к определенным интегралам и учитывая, что

,

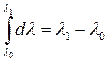окончательно получаем

. (2.20)

Второе слагаемое в квадратных скобках этой формулы, учитывающее сферичность Земли, составляет менее 1% от первого. Поэтому его можно вычислять по приближенной формуле, полученной на основе разложения логарифмической функции в ряд Тейлора

.

При такой замене относительная погрешность определения разности долгот не превысит 0,005% и уравнение локсодромии примет более простой вид:

(2.21)

Если начальная точка находится на экваторе, т.е. φ₀=0, то

. (2.22)

Для сферы е=0 и уравнение локсодромии имеет еще более простой вид (при φ₀=0):

. (3.23)

Локсодромия обычно представляет собой линию пути судна, поэтому в уравнениях (2.20)÷(2.23) при увеличении φ, монотонно возрастают и могут достигать столь угодно больших значений, вследствие чего λ₁ увеличивается на 2Π бесконечное число раз. Это значит, что локсодромия на поверхности эллипсоида или шара является спиралеобразной кривой, асимптотически приближающейся к полюсу. В частных случаях, когда А=0 или 180⁰ локсодромия совпадает с меридианом; если же А=90 или 270⁰, то локсодромия совпадает с параллелью.

Локсодромия длиннее ортодромии, проходящей через те же две точки на поверхности Земли (за исключением тех случаев, когда локсодромия совпадает с меридианом или экватором). Но на расстояниях в несколько сот миль разность длин локсодромии и ортодромии незначительна. Поэтому по морям суда всегда плавают по локсодромии, а при переходах через океан рассчитывают ряд точек ортодромии, которые затем соединяют локсодромиями и по ним совершают переход.