Дельта-правило Видроу-Хоффа
В необученной сети связям присвоены случайно выбранные небольшие по значению веса. Разность между известным значением результата и реакцией сети соответствует величине ошибки, которая может использоваться для корректировки весов межнейронных связей. Корректировка заключается в небольшом (обычно менее 1%) увеличении синаптического веса тех связей, которые усиливают правильные реакции, и уменьшении тех, которые способствуют ошибочным.
Введём следующие обозначения:
X – входной вектор из внешней среды;
Y – фактический отклик персептрона;
D – desired output – желаемый отклик персептрона.
Сигнал ошибки инициализирует процедуру их изменения, которая направлена на приближение фактического отклика к желаемому. Если персептрон содержит k нейронов, то векторы в выражении Y и D имеют размерность k, и каждая координата соответствует одному нейрону. В процессе обучения осуществляется минимизация энергии полной ошибки, т.е. суммы ошибок по всем образцам, представленным сети на этапе обучения:
(3.1)
Где р – номер образца,
k – размерность векторов Y и D.
Среднеквадратическая энергия ошибки – энергия ошибки в расчёте на один пример:
(3.2)
Где M – количество обучающих примеров.
Время, в течение которого через сеть прогоняются все примеры из обучающей выборки, назывется эпохой.
Минимизация функции осуществляется по дельта-правилу, или правилу Видроу-Хоффа. Обозначим wji(n) текущее значение синаптического веса wji нейрона i, соответствующего входу xj на шаге обучения n. В соответствии с дельта-правилом, изменение синаптического веса задается выражением:
(3.3)
Где η – положительная константа, влияющая на скорость обучения.
Данное правило легко выводится в случае линейной передаточной функции нейронов. Уравнение полной ошибки задаёт многомерную поверхность. В процессе обучения сеть изменяет весовые коэффициенты так, что осуществляется градиентный спуск по поверхности ошибок. Градиент поверхности ошибок по весовым коэффициентам выражается следующим образом:
(3.4)
Так как:
; (3.5)
. (3.6)
Обозначив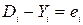 
, получим выражение градиента поверхности ошибок:
. (3.7)
Градиент указывает направление, в котором скорость нарастания функции ошибки максимальна. Умножая градиент на скорость обучения, а также учитывая, что движение по поверхности ошибки осуществляется в сторону антиградиента (ведь ищем минимум, не так ли?), получаем:
(3.8)
Вербально дельта-правило можно определить следующим образом:
Корректировка, применяемая к синаптическому весу нейрона, пропорциональна произведению сигнала ошибки на входной сигнал, его вызвавший:
(3.9)
Пошаговая корректировка синаптических весов нейрона к продолжается до тех пор, пока сеть не достигнет устойчивого состояния, при котором значения весов практически стабилизируются. В этой точке процесс обучения останавливается.
Обучение на примерах характеризуется тремя основными свойствами: емкостью, сложностью образцов и вычислительной сложностью. Емкость соответствует количеству образцов, которые может запомнить сеть. Сложность образцов определяет способности нейронной сети к обучению. В частности, при обучении ИНС могут возникать состояния «перетренировки» («переобучение»), в которых сеть хорошо функционирует на примерах обучающей выборки, но не справляется с новыми примерами, утрачивая способность обучаться.