ЗАДАЧИ И МЕТОДЫ СТАТИСТИЧЕСКОЙ ОБРАБОТКИ РЕЗУЛЬТАТОВ НАБЛЮДЕНИЙ
В общем случае любой сложный объект (систему) схематически можно представить в виде "черного" ящика, т.е. объекта, о котором известны лишь входные воздействия и выходная реакция, но неизвестны закономерности, по которым происходят преобразования "входа" в "выход" (рис. 1.1).
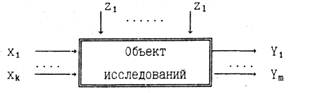
Рис 1.1.
Здесь Х={х1,...,xk) - входные управляемые контролируемые факторы, значения которых можно измерить и величиной которых можно целенаправленно управлять (расход топлива в технологических процессах, число каналов, интенсивность обслуживания в системах массового обслуживания и т.д.);
Z=(Z1,...,Zi) - неконтролируемые (неопределенные) факторы, характеризующие возмущения, действующие на объект, которые не могут быть измерены количественно (примеси в смеси, возмущения внешней среды, отказы в системе и т.п.);
Y=(y1,...,ym) - выходные показатели, характеризующие качество работы системы, рассматриваемые как оптимизируемые при выборе наилучшего режима работы системы. В общем случае они могут носить как качественный, так и количественный характер (прибыль, надежность, объем выпуска продукции, боевая эффективность, удовлетворительное/неудовлетворительное выполнение задачи, стоящей перед системой и т.п.). За счет наличия неконтролируемых факторов Z значения выходных переменных Y случайны и изменяются от наблюдения к наблюдению при одних и тех же значениях входных переменных X. Значения выходных показателей должны измеряться (вычисляться) с некоторой точностью (погрешностью).
При проведении статистического анализа результатов наблюдений над системой возникающие задачи можно условно разделить на три группы:
- оценивание тех или иных параметров и числовых характеристик случайных величин и/или законов их распределения для выходных параметров Y системы;
- построение и анализ статистических зависимостей между входными X и выходными Y переменными системы;
- проверка статистических гипотез о значениях параметров, виде закона распределения, существенности влияния входных переменных на выходные и др.
Используемые при этом методы математической статистики базируются на ограниченном числе наблюдений за поведением системы, и качество выводов зависит от объема случайной выборки. При этом используются как параметрические, так и непараметрические методы статистической обработки [6,7].
Параметрические методы основаны на использовании для описания случайных величин, описывающих результаты наблюдений за системой, т.н. параметрических законов распределения, т.е. законов, использующих задание параметров при их описании. При этом в качестве таких параметров в статистике, как правило, используются их оценки, вычисляемые по результатам наблюдений. Наиболее широко на практике используется нормальный закон распределения.
Непараметрические методы - используют при проведении стат.исследований применение непараметрических законов распределения. К таким законам относятся ранговые, порядковые статистики.
При использовании параметрических методов наибольшее распространение получили законы распределения случайных величин, которые могут быть получены как некоторые функции от других случайных величин, распределенных по нормальному закону. Это распределения 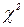 (хи-квадрат), t (Стьюдента) и F (Снедекора).
(хи-квадрат), t (Стьюдента) и F (Снедекора).