События и действия над ними

 

Событием называется любое подмножество множества W. События обозначаются заглавными латинскими: буквами А, В, С.…

Элементарный исход – это пример события. Элементарный исход, входящийвсобытие (множество) А, называется благоприятствующим событию A; соответственно определяются неблагоприятствующие событию A элементарные исходы.

Говорят, что событие A произошло, есливрезультате эксперимента произошел элементарный исход, благоприятствующий событию А.

Пустое множество Æ называется невозможным событием; оно не содержит ни одного элементарного исхода и, значит, не может произойти.

Пространство элементарных исходов W называется достоверным событием. Оно содержит все элементарные исходы и, следовательно, всегда происходит.

Любое другое событие A называется случайным, так как заранее нельзя сказать, произойдет оно или нет.

Событием, противоположным событию A (обозначается Ā), называется событие, которое содержит те и только те элементарные исходы, которые не входятв А. Если произошло событие А, то не произошло Ā, и наоборот. Ясно, что .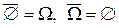

Суммой двух событий A и B (обозначается A + В) называется событие, которое содержит те и только те элементарные исходы, которые входят по крайней мереводно из событий: A или В.

Сумма событий – это объединение множеств. Событие A + B происходит тогда и только тогда, когда происходит, по крайней мере, одно из событий (либо А, либо В), либо оба сразу. Понятие суммы событий легко распространяется на любое число слагаемых.

В устной и письменной речи для обозначения суммы событий употребляют союзы «или», «либо».

Произведением событий A и B (обозначается AB) называется событие, которое содержит те и только те элементарные исходы, которые входятвоба события A и В.

Произведение событий – это пересечение множеств. Событие АВ происходит тогда и только тогда, когда происходят сразу оба события A и В. Операция произведения легко распространяется на любое число сомножителей. При словесном описании произведения событий употребляют союз «и».

Сумму и произведение n событий (бесконечного числа событий) будем обозначать так: .

События A и B называются несовместными, если их произведение – невозможное событие, AB = Æ. Вместе эти события не могут произойти.Bпротивном случае A и B называются совместными.

Говорят, что событие A влечет событие В, если все элементарные исходы, благоприятствующие А, благоприятствуют и B (множество A есть подмножество множества В). Обозначается A Í B. Ясно, что если A Í B, то AB = А, A + B = В.

Разностью событий A и B (обозначается А\В) называется событие, содержащее те и только те элементарные исходы, которые входятвсобытие А, но не входятвсобытие В. Разность событий – это разность множеств. Событие А\В происходит тогда и только тогда, когда происходит событие А, но не происходит событие В. Легко видеть, что 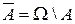. Сами элементарные исходы будем обозначать ω.