Важнейшие равносильности алгебры логики.

Рассмотрим важнейшие равносильности алгебры логики, которые можно разбить на три основные группы.

 

I группа. Основные равносильности .

 

1) x Щ x є x; x Ъ x є x – законы идемпотентности;

2) x Щ 1 є x; x Ъ 1 є 1;

3) x Щ 0 є 0; x Ъ 0 є x.

4) x Щ`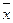є 0 – закон противоречия; x Ъ`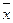є 1 – закон исключения третьего;

5) 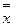- закон снятия двойного отрицания;

6) законы поглощения:

x Щ (x Ъ y) є x,

x Ъ (x Щ y) є x.

Доказать справедливость каждого тождества можно, построив таблицы истинности. Например, докажем справедливость закона поглощения относительно дизъюнкции. Таблица истинности будет содержать 4 строки:

 

х	у	уvx	х(уvx)

 

Сравнивая значения последнего столбца с соответствующими значениями высказывания х можно сделать вывод о справедливости тождества.

 

II группа. Равносильности, выражающие одни логические операции через другие.

1) x ® y є`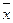Ъ y;

2) x « y є (x ® y) Щ (y ® x);

3) Закон де Моргана (закон инверсии или отрицания):

 

 

 

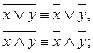
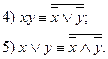
4) и 5) тождества докажем, применив закон двойного отрицания и тождества 3) второй группы:

 

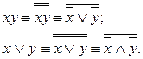
Докажем, составив таблицу истинности справедливость тождества 2):

 

х	у	х«у	х®у	у®х	(х®у)( у®х)

 

Сравнивая значения третьего столбца и последнего приходим к выводу о справедливости тождества.

 

III группа. Основные законы алгебры логики.

 

1) коммутативность:

x Щ y є y Щ x,

x Ú y º y Ú x;

2) ассоциативность:

x Щ (y Щ z) є (x Щ y) Щ z

x Ъ (y Ъ z) є (x Ъ y) Ъ z

3) дистрибутивность:

x Щ (y v z) є x Щ y Ъ x Щ z – относительно дизъюнкции,

x Ъ (y Щ z) є (x Ъ y) Щ (x Ъ z) – относительно конъюнкции.

 

Докажем справедливость дистрибутивности относительно конъюнкции. Составим таблицу истинности, которая содержит 2³ = 8 строк:

 

х	у	z	yz	x v yz	x v y	x v z	(x v y)( x v z)