Лекция №4 Векторное и смешанное произведение векторов.

I Векторное произведение

ОпределениеВекторы ,и называются коллинеарными, если они лежат в одной плоскости или в параллельных плоскостях.

 

Определение Тройка векторов называется упорядоченной, если указано какой из них считается первым, какой – вторым, какой – третий

(,,)

 

Определение Упорядоченная тройка векторов неколлинеарных называется правой, если после приведения их к общему началу, из конца третьего вектора кратчайший поворот от первого ко второму виден совершающимся против часовой стрелки. В противном случае тройка векторов называется левой.

 

ОпределениеВекторным произведением вектора на вектор называется вектор х, который определяется тремя условиями:

- длина вектора 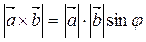, где j - угол между векторами и

- вектор хперпендикулярен каждому из векторов и

- векторы , и хобразуют правую тройку векторов.

 

Свойства векторного произведения.

- х=0, если и - коллинеарные.

- Длина векторного произведения неколлинеарных векторов и равна площади параллелограмма, построенного на этих векторах

- х= - х

- (l)х=l(х)

- (+)х= х+х

 

Выражение векторного произведения через координаты.

Т Если векторы и заданы своими координатами (x1, y1, z1) (x2, y2, z2), то векторное произведение определяется формулой:

х=( (y1z2-y2z1); (z1x2-z2x1); (x1y2-x2y1) )

 

Эту формулу можно записать с помощью определителей:

 

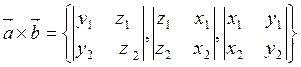
II Смешанное произведение трех векторов.

Определение Смешанным произведением трех векторов ,и называется число, равное скалярному произведению вектора на векторное произведение векторов и , т.е. . (х)

 

Т1 Смешанное произведение . (х) равное объему параллелепипеда, построенного на векторах ,и , взятому со знаком +, если тройка ,и - правая, и со знаком -, если левая.

 

Следствие . (х)=(х).

 

Т2 Если векторы ,и заданы своими координатами (x1, y1, z1) (x2, y2, z2) (x3, y3, z3), то

. (х)==

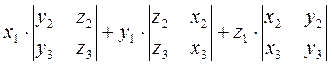=x1(y2z3-y3z2)+y1(z2y3-x3y2)+z1(x2y3-x3y2)