Основные типы распределений ДСВ.
1) Равномерное дискретное распределение.
Пусть случайная величина Х принимает в результате опыта n различных значений с равными вероятностями. Говорят, что случайная величина Х имеет равномерное дискретное распределение.
Ряд распределения:
| 
| … | 
|
|
| … |
|
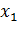
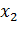
P(X=
Проверка: 
, 
Математическое ожидание:
– среднее арифметическое возможных значений.
Таким образом: 
.
Дисперсия:
– среднее арифметическое квадратов возможных значений.
Таким образом: 
Пример:
Пусть Х - число очков, выпавших при бросании игрального кубика.
|
|
|
|
|
|
2) Геометрическое распределение.
Производится ряд независимых опытов, в каждом из которых событие А может наступить с вероятностью р (не наступить - с вероятностью q=1-p).
Опыты продолжаются до первого появления события А – «до первого успеха».
Случайная величина Х - число произведённых опытов. Говорят, что Х имеет геометрическое распределение.
Ряд распределения:
| … | i | … | ||
| p | q∙p | … | 
| … |
P(X=
Проверка:
(выражение в скобках представляет собой бесконечно убывающую геометрическую прогрессию, знаменатель которой равен 
Математическое ожидание:
Таким образом, 
.
Дисперсия:
Можно показать, что 
.
Замечание:
Гипергеометрическое распределение имеет случайная величина Х - число объектов, обладающих заданным свойством, среди k объектов, случайно извлеченных (без возврата) из совокупности n объектов, ℓ из которых обладают этим свойством.
Можно показать:
математическое ожидание 
;
дисперсия 
.
Гипергеометрическое распределение широко используется в практике статистического приемного контроля качества промышленной прдукции, в задачах, связанных с организацией выборочных обследований …
3) Распределение Бернулли (биномиальное распределение).
Случайная величина Х - это число появлений события А в n независимых испытаниях, проводимых в одинаковых условиях – «число успехов».
Вероятность появления события А в каждом испытании постоянна и равна p (вероятность не появления q=1-p).
Ряд распределения:
| … | m | … | n | ||
| 
| … | 
| … | 
|
Вероятности возможных значений случайной величины Х определяются по формуле Бернулли: 
Проверка: 
Для определения числовых характеристик введём в рассмотрение случайную величину 
– число «успехов» в i-ом испытании.
| q | p |
Так как испытания независимые, а случайная величина 
, то, пользуясь свойствами математического ожидания и дисперсии, можно получить:
математическое ожидание 
,
дисперсия 
.
Пример:
Случайная величина Х – число промахов при 50 независимых друг от друга выстрелах. Вероятность промаха 0,06. Найти числовые характеристики распределения случайной величины Х.
Случайная величина Х имеет биномиальное распределение. Тогда:
4) Пуассоновское распределение.
Рассмотрим случайную величину Х, которая может принимать только целые неотрицательные возможные значения 0,1,2,…(последовательность этих значений теоретически не ограничена). Говорят, что случайная величина Х распределена по пуассоновскому закону, если вероятности возможных значений находятся по формуле Пуассона: 
где 
- некоторая положительная величина, называемая параметром пуассоновского распределения.
Ряд распределения:
| … | m | … | |||
| 
| 
| … | 
| … |
Проверка:
Математическое ожидание:
Таким образом, 
.
Дисперсия:
Можно показать, что 
.
Пример:
Число вызовов Х, поступающих на АТС за 1 минуту имеет пуассоновское распределение. Среднее число вызовов, поступающих за 1 минуту равно 1,5. Найти вероятность того, что за 1 минуту поступит не менее двух вызовов.
λ=1,5. 
Замечание: пуассоновское распределение возникает при условии проведения опыта по схеме Бернулли, когда n 
, 
пр
Так как 
мало, то закон распределения Пуассона часто называют законом редких явлений.