Электрическое поле в вакууме.
При определенных условиях тела приобретают электрический заряд (например, при трении). Наличие электрического заряда проявляется в том, что заряженное тело взаимодействует с другими заряженными телами.
Существует два вида зарядов, условно названные положительными и отрицательными. Заряды одного вида отталкиваются, разных видов – притягиваются.
Единица измерения заряда – Кулон (Кл) [q] = Кл
Всякий заряд образуется совокупностью элементарных зарядов, равных по модулю заряду электрона 1,6*10-19 Кл.
Закон сохранения заряда: алгебраическая сумма электрических зарядов любой замкнутой системы (системы, не обменивающейся зарядами с внешними телами) остается неизменной, какие бы процессы не происходили внутри этой системы.
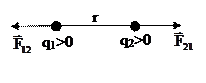 Закон Кулона: сила взаимодействия F точечных неподвижных зарядов q1 и q2 прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния r между ними.
Закон Кулона: сила взаимодействия F точечных неподвижных зарядов q1 и q2 прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния r между ними.
 , где 4p – константы (p = 3,14)
, где 4p – константы (p = 3,14)
ε0 – диэлектрическая проницаемость вакуума ε0 = 8,85*10-12 Ф/м
ε – диэлектрическая проницаемость среды.
Сила направлена по прямой, соединяющей заряды.
Вокруг неподвижного заряда существует силовое поле, называемое электростатическим полем. Его можно обнаружить, внеся в пространство другой заряд.
Основными характеристиками электростатического поля являются напряженность и потенциал.
Напряженность электростатического поля  (силовая характеристика поля) в данной точке– физическая величина, численно равная силе, действующей со стороны электрического поля на единичный положительный заряд, помещенный в эту точку поля.
(силовая характеристика поля) в данной точке– физическая величина, численно равная силе, действующей со стороны электрического поля на единичный положительный заряд, помещенный в эту точку поля.
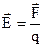
Единица измерения Вольт на метр [Е]=В/м.
Напряженность поля точечного заряда q на расстоянии r от него 
Потенциал электростатического поля j (энергетическая характеристика) в данной точке – физическая величина, численно равная потенциальной энергии, которой обладает единичный положительный заряд, помещенный в эту точку поля.

Единица измерения Вольт (в)
Также потенциал можно определить через работу
Потенциал электростатического поля j (энергетическая характеристика) некоторой точки поля – физическая величина, численно равная работе сил поля по перемещению единичного положительного заряда из данной точки в бесконечность, потенциал которой считается равной нулю.

Потенциал поля точечного заряда q на расстоянии r от него 
Напряженность и потенциал связаны соотношением
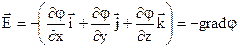
Градиент – это производная по направлению. Знак «-» означает, что вектор напряженности направлен в сторону убывания потенциала.
Если электрическое поле создается несколькими зарядами, то поле каждого из них можно рассматривать независимо от других полей, они не «мешают» друг другу.
Принцип суперпозиции: напряженность  результирующего поля, создаваемого системой зарядов, равна векторной сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
результирующего поля, создаваемого системой зарядов, равна векторной сумме напряженностей полей, создаваемых в данной точке каждым из зарядов в отдельности.
Потенциал j результирующего поля, создаваемого системой зарядов, равен алгебраической сумме потенциалов полей, создаваемых в данной точке каждым из зарядов в отдельности.
Для графического изображения электростатического поля используют силовые линии и эквипотенциальные поверхности.
Силовые линии – это линии, касательные к которым в каждой точке совпадают по направлению с вектором напряженности Е.
Силовые линии начинаются на положительных, а заканчиваются на отрицательных зарядах.
Эквипотенциальные поверхности – поверхности, в каждой точке которых потенциал имеет одно и то же значение.
 Силовые линии всегда нормальны (перпендикулярны) к эквипотенциальным поверхностям.
Силовые линии всегда нормальны (перпендикулярны) к эквипотенциальным поверхностям.
Например:
Если напряженность в каждой точке поля постоянна по величине и направлению, то такое поле называют однородным (например, поле внутри плоского конденсатора).
Поток dФ вектора напряженности  через малую площадку
через малую площадку 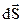 есть скалярное произведение векторов
есть скалярное произведение векторов  и
и 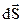 .
.
Под вектором 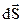 понимается вектор, направленный перпендикулярно поверхности, равный по модулю площади этой поверхности.
понимается вектор, направленный перпендикулярно поверхности, равный по модулю площади этой поверхности.
 , где a - угол, между вектором напряженности и нормалью к поверхности.
, где a - угол, между вектором напряженности и нормалью к поверхности.
Поток Ф вектора напряженности через произвольную поверхность равен интегралу по поверхности

Теорема Остроградского-Гаусса: поток вектора напряженности через произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на ε0.
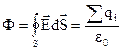
С помощью теоремы Остроградского – Гаусса можно легко рассчитать напряженности некоторых полей, например,
поле бесконечной заряженной плоскости 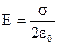 , где s - поверхностная плотность заряда на плоскости (заряд единицы площади) s=q/S
, где s - поверхностная плотность заряда на плоскости (заряд единицы площади) s=q/S
поле бесконечно длинной заряженной нити  , τ – линейная плотность заряда на нити (заряд единицы длины) τ=q/S; r – расстояние от нити до точки, в которой определяется напряженность.
, τ – линейная плотность заряда на нити (заряд единицы длины) τ=q/S; r – расстояние от нити до точки, в которой определяется напряженность.
Работа электрического поля по перемещению заряда q из точки 1 в точку 2
 , где j1, j2 – потенциалы точек 1 и 2 соответственно.
, где j1, j2 – потенциалы точек 1 и 2 соответственно.