Структура волновой функции бариона в КХД.

Появление нового квантового числа цвет позволяет полностью объяснить все трехкварковые комбинации, присущие различным супермультиплетам барионов. Ниже в конце этого раздела, мы дадим ряд примеров, относящихся к рассмотренным ранее в Лекции 9 октету (J^p=1/2⁺) и декуплету (3/2⁺) легчайших барионов. Однако перед этим мы рассмотрим общий вид волновой функции системы фермионов, введем обобщенный принцип Паули и запишем волновую функцию бариона в том виде, который непосредственно отражает свойства симметрии этой функции к перестановке тождественных кварков.

Волновую функцию системы частиц Y(1,2,3,...) можно представить в виде произведения волновых функций отдельных частиц Y₁, Y₂, Y₃, ...

 

Y(1,2,3, ...) = Y₁×Y₂×Y₃..., (10.8)

либо в виде линейной комбинации этих произведений. Здесь под цифрами 1, 2, 3, ..., помимо номера частицы, будем понимать всю совокупность координат и квантовых чисел, характеризующих состояние частицы. Далее для определенности будем говорить о системах, состоящих из трех частиц. Тогда

Y(1,2,3) = Y₁×Y₂×Y₃, (10.9)

где волновая функция отдельной частицы, например, первой

Y₁ = j₁×y(). (10.10)

j₁ описывает внутреннее состояние частицы, y(₁) - её движение как целого бесструктурного (точечного) объекта по некоторой траектории (орбите). Для точечной частицы j₁ определяется внутренними квантовыми числами такими, например, как спин, изоспин, цвет (для кварков). Соответствующее внутреннее состояние (спиновое, изоспиновое, цветовое) описывается своей волновой функцией (спиновой S, изоспиновой I, цветовой C), вид которых для данного рассмотрения не важен. j₁ - произведение этих функций

j₁ = S₁×I₁×C₁. (10.11)

Ограничимся пока одной внутренней степенью свободы - спином, тогда

Y(1,2,3) = S₁y(₁)×S₂y(₂)×S₃y(₃). (10.12)

Далее будем считать, что система состоит из трех точечных фермионов, из которых первые два тождественны (третий может быть тождествен первым двум или быть другим фермионом). Перепишем (10.12) в виде

Y(1,2,3) = Y₃ = Y(1,2)…………………Y₃, (10.13)

где

Y(1,2) = S₁S₂y(₁)y(₂) = S(1,2)y(1,2), (10.14)

и в дальнейшем будем рассматривать свойства Y(1,2,3) к перестановке двух первых (тождественных) фермионов, полагая, что спин этих фермионов 1/2. Эта перестановка затрагивает лишь функцию Y(1,2) двух тождественных фермионов. Её зависящая от пространственных координат часть 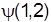=y(₁)y(₂) в системе центра инерции представима в виде

 

, (10.15)

где 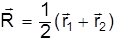- "координата" центра инерции, а - "относительная координата". - описывает движение центра инерции системы, а - относительное движение частиц системы.

Волновая функция тождественных фермионов Y(1,2) должна быть антисимметрична к перестановке частиц

 

Y(2,1) = - Y(1,2). (10.16)

При такой перестановке меняются местами не только пространственные координаты частиц, но и все их квантовые числа, т.е. имеем

Y(2,1) = S(2,1)y(2,1) = -S(1,2)y(1,2). (10.17)

Таким образом, чтобы быть антисимметричной в целом, волновая функция двух тождественных фермионов должна при их перестановке менять знак либо спиновой, либо пространственной части. Т.е. одна из компонент волновой функции должна быть симметричной (s), а другая - антисимметричной (а)

 

. (10.18)

Свойство симметрии к перестановке пространственной функции y(1,2) зависит от относительного орбитального момента L частиц. Действительно в СЦИ имеем (10.15) и

 

, (10.19)

т.е. перестановка пространственных координат сводится к операции инверсии для функции относительного движения частиц:

, (10.20)

где (-1)^L - орбитальная четность (Лекция 3). Итак, пространственная волновая функция y(1,2) симметрична (четна) при L=0,2,4... и антисимметрична (нечетна) при L=1,3,5... .

При рассмотрении спиновой части волновой функции двух фермионов ограничимся частицами со спинами 1/2. Тогда возникает лишь два варианта спиновых состояний - спины частиц параллельны (­­) и результирующий спин равен 1 или спины частиц антипараллельны (­¯) и результирующий спин равен нулю. В первом случае спиновая функция симметрична к перестановке, во втором - антисимметрична, т.е.

S_s(1,2) = S(­­), (10.21)

S_a(1,2) = S(­¯).

Теперь мы можем записать волновую функцию бариона как системы из трех кварков, используя (10.9)-(10.14). В этих выражениях вместо спиновых функций кварков S используем функции внутреннего состояния кварков j в форме (10.11), учитывающей также изоспиновую и цветовую степени свободы, присущие кваркам. Имеем

 

Y(1,2,3) = ×

= S(1,2)I(1,2)C(1,2)y(1,2)…………………Y₃. (10.22)

Функция Y(1,2,3) может быть записана и в следующем виде

Y(1,2,3) = S(1,2,3)I(1,2,3)C(1,2,3)y(1,2,3)……………, (10.23)

где S(1,2,3)=S₁×S₂×S₃, I(1,2,3)=I₁×I₂×I₃, C(1,2,3)=C₁×C₂×C₃, y(1,2,3)= =.

Если среди трех кварков, входящих в состав бариона, есть хотя

бы два тождественных, то Y(1,2,3) должна быть антисимметрична к перестановке этих кварков. При этом спиновая (S), изоспиновая (I), цветовая (C) и пространственная (y) функции по отдельности могут быть как симметричными (s) так и антисимметричными (а). Важно, чтобы Y(1,2,3) была антисимметричной в целом. В этом суть обобщенного принципа Паули. Не участвующая в перестановке частица ведет себя как наблюдатель. Ее волновая функция не меняется.

Необходимо уточнить, что понимается под тождественными кварками. Поскольку используется изоспиновое квантовое число, то кварки u и d считаются тождественными. Они составляют изодублет (I=1/2) и отличаются третьей проекцией изоспина (I₃=+1/2 для u-кварка; I₃=-1/2 для d-кварка). Использование изоспиновой симметрии превращает u и d - кварки в два состояния одной частицы - легкого кварка. Подобным образом нейтрон и протон - просто два изоспиновых состояния одной частицы - нуклона. Легкий кварк (u,d) и остальные кварки (s,c,b,t) не являются тождественными фермионами.

Изменим обозначение волновых функций в (10.23):

S(1,2,3) = y(S₁S₂S₃),

I(1,2,3) = y(I₁I₂I₃),

C(1,2,3) = y(КЗС), (10.24)

y(1,2,3) = y(r₁r₂r₃),

понимая под символами в скобках значения квантовых чисел и координат кварков. Тогда (10.23) переписывается в более удобном виде

Y(1,2,3) = y(КЗС)×y(r₁r₂r₃)×y(S₁S₂S₃)×y(I₁I₂I₃). (10.25)

Еще раз подчеркнем, что Y(1,2,3) должна быть антисимметричной в целом к перестановке всех квантовых чисел и координат двух тождественных кварков (кварки u и d тождественны). При этом цветовая, пространственная, спиновая и изоспиновая функции в отдельности могут быть как симметричными (s), так и антисимметричными (a). Перестановочный характер пространственной функции y(r₁r₂r₃) легко установить, зная орбитальный момент L кварков (10.20). Для спиновой и изоспиновой функций правило простое - если переставляются частицы с параллельными спинами (изоспинами) -(­­), то функция симметрична, если переставляются частицы с антипараллельными спинами (изоспинами) - (­¯), то функция антисимметрична. Цветовая функция y(КЗС) всегда антисимметрична (она обеспечивает выполнение принципа Паули, когда все другие квантовые характеристики тождественных фермионов совпадают). Для легчайших барионов орбитальные моменты кварков L=0 и пространственная функция y(r₁r₂r₃) - симметрична. В этом частном случае, который для нас интересен, (10.25) переписывается в виде

 

Y_a(1,2,3) = y_a(КЗС)×y_s(r₁r₂r₃)×y(S₁S₂S₃)×y(I₁I₂I₃). (10.26)

Отсюда следует, что в супермультиплетах легчайших барионов

(например, октете J^p=1/2⁺ и декуплете J^p=3/2⁺ (Лекция 9)) допустимы лишь такие кварковые комбинации, у которых спиновая и изоспиновая функции одновременно либо симметричны, либо антисимметричны, т.е. спиново-изоспиновая функция либо y_s(S₁S₂S₃)×y_s(I₁I₂I₃), либо y_a(S₁S₂S₃)y_a(I₁I₂I₃).

Рассмотрим примеры.

Пример 1. Показать, что для частиц октета легчайших барионов J^p=1/2⁺ выполняется следующее правило: у кварков одинакового аромата спины параллельны.

 

Рассмотрим протон (uud). Запишем (10.26) в виде:

Y_a(uud) = y_a(u_кu_зd_с)×y_s(r_ur_ur_d)×y(S_uS_uS_d)×y(+;+;-).

В изоспиновой функции указаны проекции изоспина кварков в зарядовом пространстве. Переставим u-кварки. Изоспиновая функция к такой перестановке симметрична. Значит должна быть симметричной и спиновая функция. Это означает, что спины u-кварков обязаны быть параллельны. Спин d-кварка должен быть антипараллелен спинам u-кварков, чтобы результирующий момент протона (его спин) был равен 1/2 (напомним, что орбитальный момент кварков в протоне равен 0). Итак, y(S_uS_uS_d)= y(­­¯). Эту ситуацию можно изобразить и так p=u_­u_­d_¯. Аналогично рассуждая, можно получить n=u_¯d_­d_­, X^o=u_¯s_­s_­, X^-= d_¯s_­s_­.

Пример 2. Показать, что в супермультиплете легчайших барионов 1/2⁺ не может быть частиц, состоящих из кварков одинакового аромата uuu, ddd, sss.

Рассмотрим комбинацию uuu

Y_a(uuu) = y_a(u_кu_зu_с)×y_s(r_ur_ur_u)×y(­­¯)×y(+r_u)×y(­­¯)×y(+;+;+).

Изоспиновая функция симметрична к перестановке любой пары u-кварков. Поэтому симметричной обязана быть и спиновая функция. Однако, она антисимметрична к перестановке тех u-кварков у которых спины антипараллельны. Таким образом комбинация из трех одинаковых по аромату кварков в супермультиплете барионов 1/2⁺ (L=0) запрещена.

Пример 3. Показать, что система двух a-частиц может быть только в состояниях с J^p=0⁺, 2⁺, 4⁺,... .

Спин и изоспин a-частицы равны 0 (S_a=I_a=0). Поэтому волновая функция двух a-частиц имеет только пространственную часть

Y(aa)=y(r_ar_a).

a-Частицы - бозоны и Y(aa) должна быть симметричной при перестановке a-частиц. Симметричной должна быть и y(r_ar_a). Это имеет место лишь при L=0,2,4... В этом случае

.

При этом P_aa=p_a×p_a(-1)^0,2,4,...=+1.