Возбуждение автоколебаний и работа автогенератора в режиме малой амплитуды выходного сигнала

 

Важная задача – изучить условия, при которых возможно возбуждение колебаний в автогенераторе. При самовозбуждении генератора на начальном этапе развития колебательного процесса амплитуда колебаний мала. Лишь после установления колебаний в изучаемых далее автогенераторах эти колебания станут гармоническими.

Пусть управляющее напряжение в схеме автогенератора с трансформаторной связью на рис. 5.6 настолько мало, что нелинейный электронный прибор можно заменить приближенно управляемым источником тока, выходной сигнал которого линейно зависит от управляющего напряжения. Тогда нелинейное второе уравнение в системе (5.3) заменим приближенно на линейное уравнение: , где 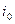- постоянная составляющая тока, 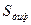- дифференциальная крутизна ВАХ прибора в фиксированной рабочей точке. Подставим выражение в первое уравнение системы (5.3). Получим линейное дифференциальное уравнение

 

(5.4)

 

где

(5.5)

 

(5.6)

Уравнению (5.4) соответствует эквивалентная схема колебательной системы автогенератора в виде колебательного контура (см. рис. 5.8).

 

Рис. 5.8

 

Здесь - дифференциальное сопротивление, вносимое в контур за счет действия обратной связи. В соответствии с (5.5) , где знак минус соответствует положительной, а знак плюс – отрицательной обратной связи. Отрицательный знак вносимого сопротивления соответствует внесению энергии колебаний в колебательный контур, а положительный знак – отбору энергии колебаний из контура за счет действия обратной связи.

Для лампового генератора с трансформаторной связью, получающегося заменой транзистора на лампу, получается дифференциальное уравнение также вида (5.4).

Линеаризация нелинейных уравнений автогенераторов – общий метод, используемый для изучения условий их самовозбуждения и работы в режиме малой амплитуды сигнала. Для изучения условий самовозбуждения можно применить теорию устойчивости линейных систем, в частности,

1) общий критерий устойчивости, основанный на изучении поведения корней характеристического уравнения системы на комплексной плоскости;

2) критерий устойчивости Рауса-Гурвица, основанный на изучении соотношений между коэффициентами характеристического уравнения;

3) критерий устойчивости Найквиста;

4) критерий Михайлова;

5) критерий Ляпунова.

Применим общий критерий устойчивости к автогенератору, показанному на рис. 5.6. Ищем решение уравнения (5.4) в виде на комплексной плоскости частоты , получаем характеристическое уравнение автогенератора:

 

(5.7)

 

корни которого равны

(5.8)

 

В соответствии с общим критерием устойчивости система неустойчива, если и (или) . Практически всегда частота заполнения колебаний, возникающих в линейном режиме, близка к собственной частоте колебательной системы автогенератора, так что . Тогда вместо (5.8) имеем: Видно, что система неустойчива по отношению к возбуждению в ней автоколебаний, если

 

(5.9)

 

При выполнении (5.9) обратная связь оказывается не только положительной, но и достаточно глубокой, чтобы компенсировать потери энергии колебаний на сопротивлении колебательного контура. Для обеспечения возможности регенерации следует выбрать согласованную намотку провода в обмотках трансформаторной связи, когда в (5.9) действует верхний знак. Самовозбуждение колебаний возможно, если выбрать

(5.10)

 

где соответствует критическому уровню магнитной связи между катушками индуктивности,

(5.11)

 

где - добротность колебательного контура без учета регенерации.

Анализ работы автогенератора в режиме малой амплитуды сигнала, то есть на начальном этапе работы после начала самовозбуждения, проводится путем интегрирования линейного дифференциального уравнения, описывающего такие колебания автогенератора. Так, для схемы рис. 5.6 искомым уравнением служит (5.4). При выполнении условия самовозбуждения (5.10) растущие экспоненциально по амплитуде со временем автоколебания описываются решением этого уравнения:

 

 

где постоянные и определяются начальными условиями.