Разностный метод

Нелинейные уравнения в частных производных с коэффициентами достаточно общего вида, а также уравнения в областях достаточно общей формы обычно не удается решить аналитическими или автомодельными методами. Основным методом их решения являются численные методы, среди которых наиболее часто используемым является разностный метод.

Для использования разностного метода в области переменных вводят некоторую сетку. Все производные, входящие в уравнение, заменяют конечными разностями значений функций в узлах сетки. Полученное в результате алгебраическое уравнение называют разностной схемой. Решая алгебраическую систему уравнений, находят приближенные (разностные) значения функции в узлах сетки. Возникают обычные вопросы при постановке вычислительного эксперимента:

· Существует ли решение алгебраической системы уравнений и является ли оно единственным?

· Каков эффективный алгоритм поиска решения?

· При каких условиях численное решение сходится к точному решению и с какой скоростью?

Есть еще пара вопросов, которые ранее в нашем практикуме не возникали. Это процедура выбора сетки и составление разностной схемы на этой сетке. Для иллюстрации последних двух вопросов рассмотрим пример.

Составим пару простейших разностных схем для линейного одномерного уравнения теплопроводности в ограниченной области G.

, (22)

. (23)

Решение уравнения теплопроводности (22) с начальными и граничными условиями (23) ищется в ограниченной области G = [0 £ x £ a] ´ [0 £ t £ T].

Введем в области G сетку, образованные пересечением прямых линий x_n = nh, n = 0,1,…, N и t_m = mt, m = 0,1,…,M. Считаем для простоты сетку равномерной по оси x и t соответственно. Величины h и t являются шагами сетки по переменным x и t соответственно (рис.5,а). Значения функции в узлах сетки представим в виде: .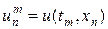


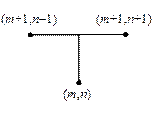
Рис.5,а. Разностная схема для задачи (22), (23)	Рис.5,б. Шаблон разностной схемы (24), (25)	Рис.5,в. Шаблон разностной схемы (26)

В начале построим разностную схему для численного решения уравнения (22) следуя конфигурации узлов на рис.5,б. В уравнении (22) заменим производную u_t на разностное отношение , а вторую производную u_xx — 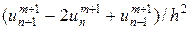. В результате можно получить разностную схему следующего вида

(24)

для приближенного решения уравнения (22). Недостающие уравнения для решения задачи (24) берутся из начальных и граничных условий (23), т.е.

. (25)

Конфигурация узлов (рис.5,б) лежащая в основе разностной схемы (24), (25) называется шаблоном.

Для одной и той же задачи можно составить множество разностных схем. Например, если в качестве шаблона разностной схемы выбрать шаблон на рис.5,в, то

. (26)

Начальные и граничные значения для разностной схемы (26) можно записать по аналогии с (25).

В дальнейшем будут рассмотрены различные способы составления и исследования разностных схем для различных типов уравнений. В дальнейших лекциях будут изложены те разностные схемы, которые хорошо себя зарекомендовали при решении тех уравнений математической физики, которые используются в задачах переноса, теплопроводности, диффузии, акустики, газодинамики, электричества и в ряде других областях.

Для большинства разностных схем узлы сетки лежат обычно на пересечении некоторых прямых линий (гиперповерхностей в многомерных задачах). Для двумерных задач в прямоугольной области наиболее часто используют прямоугольную сетку (см., например, рис.5,а). Заметно реже используют треугольную сетку (рис.6,а). Для трехмерных задача наиболее употребительна сетка из прямоугольных параллелепипедов (рис.6,б). На рис.6,в приведен пример менее употребительной трехмерной сетки, состоящей из трехгранных призм.


Рис.6,а. Пример треугольной сетки	Рис.6,б. Пример трехмерной сетки	Рис.6,в. Пример трехмерной сетки

Если одной из переменных в задаче является время t, тогда совокупность узлов сетки, на линии (гиперплоскости) t = t_m называют слоем. Узлы разностной схемы связанные друг с другом согласно шаблону называются регулярными, остальные узлы — нерегулярными. Нерегулярными обычно являются граничные узлы. Например, на рис.7,а приведен пример двумерной прямоугольной сетки, на которой построена сложная область с криволинейной границей. Жирным крестом внутри области обозначены регулярные узлы разностной схемы связанные с помощью шаблона, представленного на рис.7,б. Звездами обозначены некоторые нерегулярные узлы в окрестности криволинейной границы области.


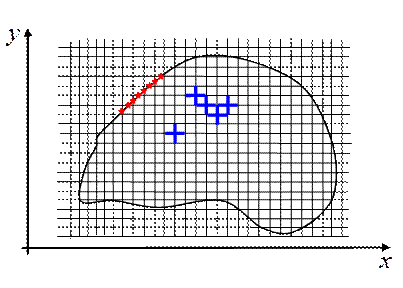
Рис.7,а. Пример сложной области и прямоугольной сетки	Рис.7,б. Шаблон разностной сетки

Вернемся к разностной схеме (26). Положим в этой схеме m = 0, т.к. известно из начального условия, можно найти при n = 1,…,N-1. Значения и находим из граничных условий (25). Тем самым значения функции на первом временной слое найдены. Аналогичная процедура может быть проделана при определении 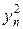и т.д. Схема, похожая на (26), т.е. такая схема, в которой значение функции на следующем слое легко выразить через значения функции на текущем слое называется явной.

Схема (24) на следующем временном слое содержит в каждом уравнении несколько неизвестных значений. Подобные схемы называют неявными. Перепишем схему (24) и граничные условия (25) в следующем виде:

(27)

На каждом слое схема (27) представляет собой систему линейных уравнений для определения неизвестных величин . Матрица данной алгебраической системы уравнений трехдиагональная и решение может быть найдено с помощью обычной алгебраической прогонки.