Автомодельные решения

Уравнения в частных производных допускают классы упрощенных решений, которые получили название автомодельных. Для решений этого класса характерна зависимость функции решения от одной переменной x, которая является специальной комбинацией t, x.

Для построения примера автомодельного решения рассмотрим одномерное квазилинейное уравнение теплопроводности, в котором коэффициент теплопроводности степенным образом зависит от температуры, т.е.

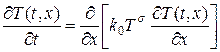, (13)

где k₀, s — некоторые неотрицательные константы. Зависимости степенного типа, подобные (13), весьма распространены в физики. Так, в физике плазмы известно, что коэффициент электронной теплопроводности пропорционален .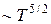

Построим автомодельное решение для уравнения (13) типа бегущей волны:

. (14)

Подставляя (14) в (13), приходим к следующему обыкновенному дифференциальному уравнению:

. (15)

Уравнение (15) можно один раз проинтегрировать. Появится константа, которую определим, предполагая, что бегущая волна двигается по нулевому температурному фону. После этих предположений возможно провести еще одно интегрирование и в окончательном виде получить:

(16)

Возвращаясь в (16) к представлению в координатах t, x, получим

(17)

Автомодельное решение (17) представляет собой температурную волну, бегущую с постоянной скоростью по нулевому температурному фону. Фронт волны имеет координату x₀ + ct. Профили волны всюду гладкий, кроме фронта волны, где производная терпит разрыв.

На листинге_№2 приведен код программы, изображающей движение бегущей волны (17).

 

Листинг_№2

%Программа изображения бегущей волны квазилинейного

%уравнения теплопроводности

%очищаем рабочее пространство

clear all

%константы уравнения теплопроводности и бегущей волны

k0=1; sigma=3; c=4; x0=0.5;

%определяем сетки по времени и пространству

t=0:0.025:1;

x=0:0.01:5;

%организуем цикл рисования профиля температуры в

%различные моменты времени

for i=1:length(t)

%определяем профиль температуры

for j=1:length(x)

T(j)=0;

if x(j)<=x0+c*t(i)

T(j)=(((c*sigma)/k0)*(x0-x(j)+...

c*t(i)))^(1/sigma);

end

end

%рисуем температурный профиль

if i==1

plot(x,T,'Color','red','LineWidth',3);

else

plot(x,T);

end

hold on

end

 

На рис.2 приведены графики, изображающие движение бегущей температурной волны. Красным цветом выделен начальный температурный профиль.

 

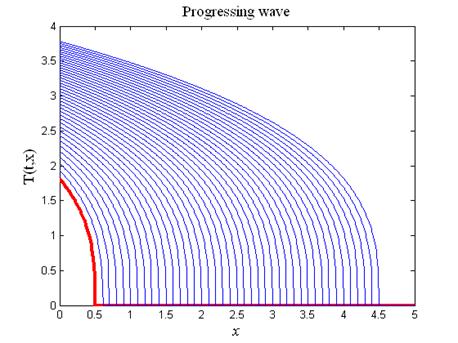
Рис.2. Изображение бегущей волны (17)

 

Рассмотрим еще один пример автомодельного решения одномерного квазилинейного уравнения теплопроводности с источником:

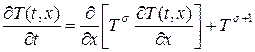. (18)

Уравнение (18) в отличие от (13) содержит источник тепла , степенным образом зависящий от температуры. Согласно исследованиям уравнения (18), проведенных в школе А.А. Самарского и С.П. Курдюмова[3], было установлено наличие так называемой “фундаментальной длины”, на которой происходит горение среды, при этом тепло не распространяется за пределы данной длины, а температура может расти неограниченно в течение конечного интервала времени. Уравнение (18) допускает специальный класс автомодельных решений, который получил название режимов с обострением.

Построим этот класс автомодельных решений. Для этого представим решение в виде:

. (19)

где t_f — время обострения или фокусировки.

Подставим (19) в (18), тогда

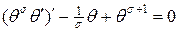. (20)

Уравнение (20) допускает следующее аналитическое решение:

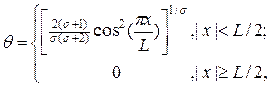(21)

где 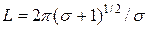— фундаментальная длина.

На листинге_№3 приведен код программы, изображающей режим с обострением (19), (21). Итоговый график вынесен на рис.3. Красным цветом на графике выделен начальный профиль.

 

Листинг_№3

%Программа изображения режима с обострением

%(19), (21)

%очищаем рабочее пространство

clear all

%определяем момент фокусировки и степень

%нелинейности sigma

tf=1; sigma=3;

%определяем фундаментальную длину

L=2*pi*sqrt(sigma+1)/sigma;

%задаем сетки по времени и по пространству

t=0.98:0.001:0.999;

x=-L:0.01:L;

%организуем цикл рисования профиля режима с

%обострением во времени

for i=1:length(t)

for j=1:length(x)

T(j)=0;

if abs(x(j))<0.5*L

T(j)=(tf-t(i))^(-1/sigma)*...

(((2*(sigma+1))/(sigma*(sigma+2)))*...

cos((pi*x(j))/L)^2)^(1/sigma);

end

end

%рисуем температурный профиль в начальный и в

%последующие моменты времени

if i==1

plot(x,T,'Color','red','LineWidth',3);

hold on

end

plo(x,T);

hold on

end

 

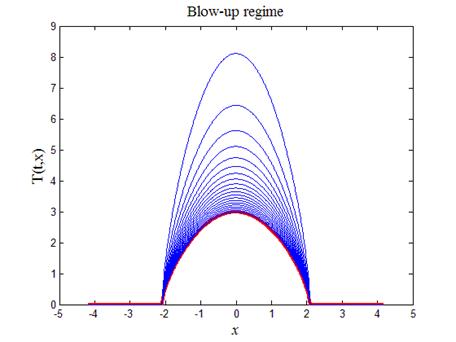
Рис.4. Режим с обострением (19), (21)