Эффект Джоуля - Томсона

Различают дифференциальный и интегральный эффекты Джоуля-Томсона. В технике для получения низких температур применяется интегральный эффект Джоуля-Томсона, но рассмотрение мы начнем с дифференциального эффекта или опытов Джоуля-Томсона (1852-1862 гг.). В этих опытах бралась цилиндрическая трубка, окруженная теплоизолирующим материалом. В середине трубки между двумя сетками MN и M1N1 (рис.2) помещалась пробка из плотной ваты или очесов шелка. Исследуемый газ под действием разности давлений медленно протекал через пробку. В этих условиях в каждый момент времени газ по обе стороны пробки находился в термодинамически равновесных состояниях. Давления газа по разные стороны пробки P1 и P2 поддерживались постоянными. При стационарном течении по одну сторону пробки устанавливалась постоянная температура газа Т1, по другую - постоянная температура Т2. Эти температуры и измерялись в опыте. Изменение температуры газа при стационарном течении газа через пробку и называется эффектом Джоуля-Томсона.

Выделим мысленно по левую сторону пробки объем газа V1 . После прохождения через пробку выделенная порция газа займет объем V2. В левой части над газом производилась работа P1V1 , в правой части газ производит работу P2V2 . Полная работа, совершенная газом, равна . Применим к выделенной порции газа первое начало термодинамики. Теплоты газ не получал, так как стенки трубки теплоизолированы, физическое состояние пробки и ее внутренняя энергия остались неизменными. Поэтому, обозначая внутреннюю энергию выделенной массы газа U , можно написать

, или (12)

.

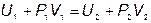По определению величина 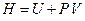есть термодинамическая функция газа, энтальпия. Поэтому последнее равенство означает, что в опыте Джоуля-Томсона энтальпия газа не меняется, т.е. .

Это соотношение является основным в теории эффекта Джоуля-Томсона. Пусть по разные стороны пробки поддерживается малая разность давлений DP. Соответствующая ей разность температур DT измеряется в опыте. Течение газа предполагается установившимся. Задача теории состоит в том, чтобы, зная DP и уравнение состояния газа, вычислить DT. Поскольку в опыте Джоуля-Томсона энтальпия H не меняется то, рассматривая ее как функцию температуры и давления, можно написать

. (13)

По определению энтальпии

.

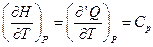Для вычисления частной производной обратимся к первому началу термодинамики, записанному в виде:

. (14)

Используя определение энтальпии , перепишем уравнение (14) следующим образом

,

или . (15)

Разделив выражение (15) на Т, получим приращение энтропии:

. (16)

Рассматривая энтропию как функцию параметров Т и Р, можно представить приращение энтропии в виде

.

Сравнение этого выражения с (16) дает, что

. (17)

Смешанные частные производные некоторой функции удовлетворяют условию

.

В соответствии с этим

.

Подстановка в это равенство выражений (17) приводит к соотношению

.

Осуществив дифференцирование, получим

.

Приняв во внимание, что , приходим к формуле

. (18)

Тогда уравнение (13) примет вид

,

откуда следует

, (19)

где CP- молярная теплоемкость газа при постоянном давлении.

При выводе (19) не предполагалось знания явного вида уравнения состояния газа. Для получения конкретных результатов надо знать уравнение состояния газа. Если газ идеальный, то для одного моля газа из уравнения Менделеева-Клапейрона имеем , и тогда 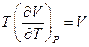, и из соотношения (19) следует , т.е. для идеального газа эффект Джоуля-Томсона не имеет места.

Но для реальных газов, вообще говоря, происходит либо нагревание, либо охлаждение. В качестве уравнения состояния реального газа возьмем уравнение Ван-дер-Ваальса:

, (20)

где a и b - константы Ван-дер-Ваальса.

Рассмотрим простейший случай разреженного газа, когда члены, содержащие a и b, являются малыми поправками. Можно ограничиться линейным приближением, отбросив все члены с высшими степенями a и b. В этом приближении соотношение (19) приводит к выражению

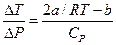. (21)

Если , то , и газ охлаждается. Если, напротив, , , 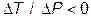и газ нагревается. В частности, при , газ всегда охлаждается; при , 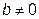- всегда нагревается. Первый результат понятен, так как при расширении кинетическая энергия теплового движения газа расходуется на работу против сил молекулярного притяжения. Второй результат не столь очевиден.

 
 

При изменение температуры равно нулю. Температура называется температурой инверсии дифференциального эффекта Джоуля-Томсона. При T < Ti в опыте Джоуля-Томсона газ охлаждается, при T > Ti газ нагревается. Для большинства газов Ti лежит значительно выше комнатной температуры. Такие газы в опыте Джоуля-Томсона охлаждаются. Для водорода и гелия Ti лежит значительно ниже комнатной температуры (Ti = - 800 C), и эти газы нагреваются.

Перейдем теперь к рассмотрению интегрального эффекта Джоуля-Томсона. Интегральный эффект Джоуля-Томсона получают, заставляя газ, находящийся под высоким давлением (порядка сотен атмосфер), перетекать в пространство с низким давлением (порядка атмосферного) через вентиль или узкое отверстие. Такой процесс называется дросселированием газа.

Изменение температуры газа T2 - T1 при интегральном эффекте определяется формулой

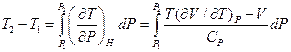. (22)

В зависимости от знака подынтегрального выражения изменение температуры T2 - T1 может быть как положительным, так и отрицательным. В частности, если во всем диапазоне давлений дифференциальный эффект приводит к DT < 0, то и интегральный эффект будет приводить к T2 - T1 < 0, т.е. в результате дросселирования газ должен охлаждаться. При комнатной температуре это имеет место для большинства газов, в частности, для воздуха и углекислоты. Совсем иначе ведет себя водород. Для него при комнатных температурах интегральный эффект Джоуля-Томсона приводит к нагреванию газа. Такое нагревание иногда приводит к катастрофам, в которых сильно сжатый водород самопроизвольно воспламеняется при истечении из поврежденных труб. При внезапном расширении водород может охлаждаться лишь тогда, когда его температура ниже минус 800 С.