Цикл Карно и его КПД
Французский инженер Сади Карно предложил идеальный цикл, который даёт максимальное КПД т.е.  . Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно.
. Этот цикл состоит из двух изотерм и двух адиабат и носит название цикла Карно.
 - изотермическое расширение при - изотермическое расширение при 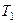 , ,
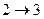 - адиабатическое расширение, - адиабатическое расширение,  , ,
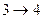 - изотермическое сжатие при - изотермическое сжатие при 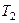 , ,
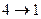 - изотермическое сжатие, - изотермическое сжатие,  . .
|

Вычислим КПД цикла Карно для идеального газа. При изотермическом процессе внутренняя энергия идеального газа остаётся постоянной. Поэтому количество полученной газом теплоты  равно работе
равно работе  , совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2). Эта работа равна
, совершаемой газом при переходе из состояния 1 в состояние 2 (рис. 2). Эта работа равна
 ,
,
где 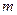 – масса идеального газа в тепловой машине.
– масса идеального газа в тепловой машине.
Количество отдаваемой холодильнику теплоты  равно работе
равно работе  , затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна
, затраченной на сжатие газа при переходе его из состояния 3 в состояние 4. Эта работа равна
 .
.
Для того чтобы цикл был замкнутым, состояние 1 и 4 должны лежать на одной и той же адиабате. Отсюда вытекает условие
 .
.
Аналогично для состояний 2 и 3 должно вытекать условие
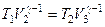 .
.
Разделив одно соотношение на другое, приходим к условию замкнутости цикла
 .
.
Теперь подставляя  и
и  в выражение для КПД, получим
в выражение для КПД, получим
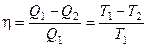 . (2)
. (2)
В результате получим формулу для КПД цикла Карно:
 ,
,
где 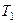 - температура нагревателя,
- температура нагревателя, 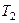 - температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах
- температура холодильника. КПД цикла Карно является максимальным КПД из всех возможных циклов, осуществляемых в данных температурных интервалах 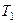 и
и 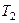 .
.
Вернёмся к соотношению (2), которое имеет место в случае обратимого цикла Карно. В общем случае при возможности необратимого цикла Карно это соотношение примет вид:
 . (3)
. (3)
Преобразуем (3) следующим образом:
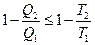 ,
,  , или
, или 
В результате получим
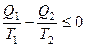 .
.
Для обратимого цикла Карно:  ,
,
для необратимого цикла Карно:  .
.
Для произвольного обратимого цикла:
 ,
,
для произвольного необратимого цикла:
 .
.