Анализ размерных связей деталей с использованием теории графов

Размерные связи машиностроительных деталей можно предста­вить графом, вершины которого обозначают элементарные поверх­ности, а ребра – размерные связи между ними:

G = (A, Е),

где А = {а_i} – множество поверхностей детали; Е = {E_ij} – мно­жество размеров, связывающих поверхности E_ij = (а_i, а_j).

Размерная цепь – это расположенная по замкнутому контуру совокупность размеров, влияющих на точность одного из размеров контура. Ввиду того, что замыкающее звено непосредствен­но при обработке не выполняется и представляет собой результат формирования всех остальных звеньев цепи, граф размерных связей детали в одном координатном направлении является деревом (рис. 3.3, а).

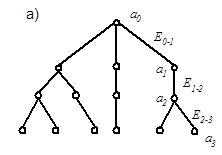Рис. 3.3. Граф размерных связей типа «дерево» (а) и «мультиграф» (б)

 

Если на чертеже детали имеются размерные связи более чем в одном координатном направлении, то граф, которым они описы­ваются, называется цепью или мультиграфом (рис. 3.3, б). На этом рисунке ребра х_1-2, x_2-4, y_1-2, z_3-10 и другие обозначают размерные связи между элементами детали по координатам X, Y, Z. На графе можно выделить несколько ветвей – маршрутов графа.

Исходя из вышеописанных особенностей теории графов, на ее основе может быть сформирована формализованная модель геометрической структуры детали. Для этого необходимо, чтобы исходная геометрическая информация о детали представляла собой полное ее описание в цифровой форме. Отсюда задача построения формализованной модели геометрической структуры детали сводится к распознаванию ее размерных связей в таблице кодированных сведений (ТКС) и построению матрицы смежности соответствующего графа.

При неавтоматизированном проектировании для распознавания размерных связей технолог визуально выявляет необходимые точностные параметры, связи между ними, размерные цепи, производит их пересчет, исходя из конкретных условий, и назначает технологи­ческий процесс изготовления детали.

В условиях автоматизированного проектирования процесс построения формализованной модели структуры детали производится путем анализа информации, содержащейся в таблице кодированных сведений, заполненной согласно принятой для данной САПР ТП системы кодирования (языка описания детали). Для решения рассматриваемой задачи ТКС должна содержать определенный набор реквизитов (сведений), которые необходимы для построения формализованной модели. К таким реквизитам, описывающим положение отдельной поверхнос­ти в общей конструкции детали, относятся:

· номер элемента НЭ,

· код элемента КЭ,

· номер базы НБ,

· линейный размер X,

· верхнее отклонение размера Х ВО,

· нижнее отклонение размера Х НО.

В результате выборки из ТКС формируется таблица, являющаяся исходной для алгоритма формирования графа размерных связей детали. Эта таблица представляет двухмерный массив М(m, п), где m=6 – число реквизитов, описывающих положение i-й поверхности; n – количество поверхностей детали.

В качестве примера рассмотрим построение графа размерных связей для детали «вал» (рис. 3.4). По вышеизложенным пра­вилам для этой детали составлена таблица выборки сведений из ТКС (табл. 3.1).

Рис. 3.4. Чертеж детали типа «вал»

 

Табл. 3.1. Таблица выборки сведений из ТКС

НЭ	КЭ	НБ	X	ВО	НО
			–28
			-24
			-68

 

Чтобы построить граф размерных связей детали в автомати­зированном режиме, необходимо сформировать матрицу смеж­ности. Для ее построения следует из множества поверхностей детали выделить базовую поверхность, которая при­нимается в качестве начальной вершины графа. Данная задача является достаточно важной, так как от нее зависит структура формализованной модели. При этом необходимо учитывать правила построения технологических процессов. Одно из таких правил определяет необходимость подготовки в первую очередь техно­логических установочных баз. Поэтому в качестве начальной верши­ны графа размерных связей используются поверхности, служащие технологическими установочными базами и обрабатываемые на первой операции. Это условие при автоматизированном проектирова­нии должно быть обязательно проверено.

В рассматриваемом примере в качестве базовой принята по­верхность с номером 1. С этой поверхности начинается формирова­ние матрицы смежности.

Граф размерных связей детали можно рассматривать состоящим из отдельных деревьев (кустов), каждый из которых имеет одну начальную (базовую) вершину и несколько (в крайнем случае, одну) висящих вершин. При формировании матрицы смежности происходит выделе­ние деревьев графа.

Алгоритм формирования графа размерных связей строится следующим образом. Для принятой базовой поверхности (началь­ной вершины графа) определяются висящие вершины первого дерева графа. С этой целью из сформированной табл. 3.1 (по третьему столбцу) выбираются номера элементов НЭ, связанные с базовой поверхностью, и заносятся в матрицу смежности графа (табл. 3.2).

 

Табл. 3.2. Матрица смежности графа

 

В этой таблице по вертикали и горизонтали матрицы обозначены номера поверхностей. Если две какие-либо поверхности имеют размерную связь или связаны конструктивно, то в клетку, располо­женную на пересечении соответствующей строки и столбца, ставится 1. При отсутствии размерной связи в клетку ставится нуль, который для упрощения таблицы может быть опущен.

После построения первого дерева графа производится формирова­ние его последующих деревьев. Для этого необходимо проверить, не является ли поверхность, соответствующая выбранной висящей вершине, базовой для других поверхностей. Если да, то повторяется последовательность выбора элементов с висящими вершинами по отношению к этой базовой поверхности.

После заполнения матрицы смежности графа и выделения его деревьев (рис. 3.5) может быть сформирован окончательный граф размерных связей (рис. 3.6).

 

 

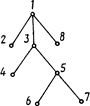
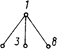
Рис. 3.5. Деревья графа размерных связей детали Рис. 3.6. Граф размерных связей детали типа <вал»

 

В памяти ЭВМ граф размерных связей детали описывается массивом (назовем его, например, ГРАФ), который используется в дальнейшем при выборе технологических баз и проектировании технологических маршрутов.