Момент инерции тела. Теорема Гюйгенса-Штейнера. Примеры вычисления моментов инерции тел
Момент инерции тела аддитивная величина, равная сумме моментов инерции всех частиц тела:
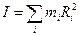 .
.
Здесь mi — масса i-той частицы, которую можно связать с плотностью вещества ri и объёмом частицы:
mi = riDVi.
Тогда 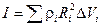 .
.
Если тело однородно, то есть его плотность повсюду одинакова, то r можно вынести за знак суммы:
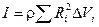 .
.
Разделяя тело на всё более мелкие частицы, сведём задачу отыскания момента инерции к вычислению интеграла:
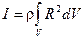 .
.
Интегрирование проводится по всему объёму тела V.
В качестве примера вычислим момент инерции тонкого однородного стержня относительно оси z, проходящей через его центр масс — точку С (рис. 9.3). Длина стержня — l, его масса — M.
На расстоянии x от оси вращения выделим элемент dx, масса которого dm = 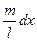 .
.
| |
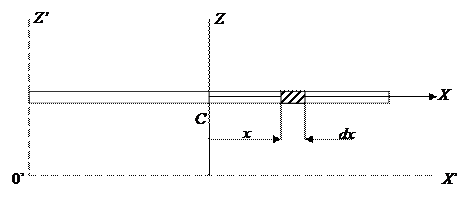
Рис. 9.3
Момент инерции этой частицы стержня равен:
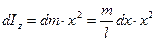 .
.
Вычислив подобным образом, моменты инерции всех элементов стержня, сложим их, взяв интеграл:
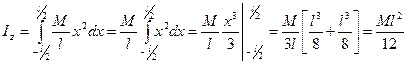 .
.
Таким образом:
Iz = 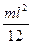 . (9.7)
. (9.7)
Интегрирование проведено по x в пределах от 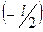 до
до 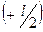 .
.
Как изменится момент инерции этого стержня, если ось вращения перенести в другое место? Провести её, например, через край стержня?
В этом случае прежний интеграл нужно рассмотреть в пределах от 0 до l:
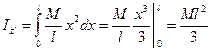 . (9.8)
. (9.8)
Новое значение момента инерции того же стержня заметно возросло. Связано это с тем, что момент инерции тела определяется не только его массой, но и её распределением относительно оси вращения.
Вычислим момент инерции ещё одного тела: сплошного цилиндра относительно его геометрической оси.
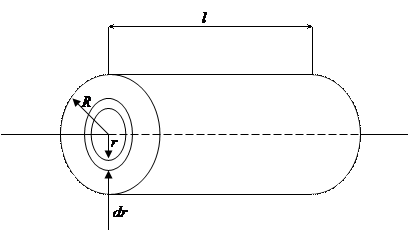
Рис. 9.4
Пусть M — масса, а R — радиус цилиндра (рис. 9.4). Выделим в этом цилиндре цилиндрический слой радиусом r и толщиной dr. Масса этого слоя:
dm = r × dV = r × 2pr × dr × l,
где: r — плотность материала цилиндра;
l — его длина.
Все частицы этого слоя находятся на одинаковом расстоянии от оси вращения — геометрической оси цилиндра, значит, момент инерции слоя равен:
dI = dm × r2 = r × 2pr × dr × l × r2.
Для отыскания момента инерции цилиндра проинтегрируем последнее выражение:
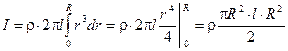 .
.
Отметим, что pR2l = V — объём цилиндра, а rpR2l = rV = M — его масса.
Тогда момент инерции цилиндра относительно его геометрической оси можно окончательно записать в таком виде:
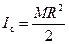 .
.