Задачи для самостоятельного решения и аудиторных занятий.

 

1. Задачи на элементы комбинаторики, классическое определение вероятности, непосредственный подсчёт вероятности.

 

1.1 13 студентов обменялись рукопожатиями. Сколько всего произошло рукопожатий? (Ответ: )

1.2 Группа студентов состоит из 25 человек. Нужно выбрать 4-х делегатов на студенческую конференцию. Сколькими способами может быть сделан этот выбор? (

1.3 В турнире участвуют 6 шахматистов. Сколькими способами эти шахматисты могут расположиться в турнирной таблице?

1.4 Сколько различных пятизначных цифр можно составить из цифр:2;4;6;8;0.

(

1.5 Сколько различных отношений можно составить из трёх данных отрезков: а;в;с? (

1.6 Сколько диагоналей в выпуклом n – угольнике? (

1.7 Имеется три флага: красный, белый, зелёный. Сколько различных сигналов можно передать, вывешивая эти флаги на мачте, если нельзя вывесить более трёх флагов? (

1.8 Сколькими способами из 15 человек можно выбрать судъю и 6 участников волейбольного матча? (

1.9 Из трёх инженеров и девяти рабочих должна быть составлена бригада в составе 7 человек. Сколькими способами может быть составлена бригада, если в неё должен входить хотя бы один инженер? (

1.10 Сколькими способами из 20 человек можно выбрать двух судий и 5 участников одной команды баскетбольного матча? (

1.11 Среди 50 электролампочек 3 нестандартные. Найти вероятность того, что две наугад взятые лампочки окажутся нестандартными? (

1.12 В цехе работает 6 мужчин и 4 женщины. По табельным номерам наудачу отобрали 7 человек. Найти вероятность того, что среди отобранных окажутся 3 женщины?

1.13 Четырёх томное сочинение расположено на полке в случайном порядке. Найти вероятность того, что тома стоят в должном порядке справа налево или слева направо?

1.14 В вещевой лотереи из 20 билетов 4 – выигрышные. Куплено 2 билета. Какова вероятность выигрыша?

 

2. Задачи на геометрическую вероятность.

 

2.1 В точке С, положениекоторой на телефонной линии АВ длины L равновозможно, произошёл разрыв, определить вероятность того, что точка С удалена от точки А на расстояние, не меньше e (e < L).

2.2 На отрезке АВ длины L поставлены наудачу две точки: C и D. Найти вероятность того, что точка С окажется ближе к точке А, чем точка D. ( 0,5).

2.3 На паркетный пол наудачу бросают монету диаметра d. Паркет имеет форму квадрата со стороной а (а > d). Какова вероятность того, что монета не пересечёт ни одной из сторон квадрата паркеты?

2.3 В области, ограниченной эллипсом разбросано 5 кружков радиуса 0,1. Известно, что кружочки не пересекаются друг с другом и с эллипсом. Какова вероятность толго, что точка, брошенная наудачу в эллипс, не попадёт ни в один из кружочков? (

2.4 Стержень длиной 200 мм наудачу ломается на три части. Найти вероятность того, что часть стержня между точками излома будет не более 10 мм?

(1-)

2.5 Два корабля должны подойти к одному и тому же причалу. Время прихода кораблей независимо и равновозможно в течение данных суток. Определить вероятность того, что одному из кораблей придётся ожидать освобождения причала, если время стоянки первого корабля 1 час, второго корабля – 2 часа.

( )

2.6 Событие, состоящее из мгновенного сигнала, должно произойти между одним и пятью часами. Какова вероятность того, что сигнал будет зафиксирован в течение 20 минут после двух часов?

 

3. Задачи на сложение, умножение событий, формула полной вероятности, формула Байеса.

Два стрелка делают по одному выстрелу. Рассматриваются события:

Что означают события: А + В; АВ; (хотя бы одно попадание; два попадания; два промаха; 1-ый попал, 2-ой - нет; первый промахнулся, второй попал; одно попадание при двух выстрелах).

Какие из перечисленных групп событий образуют ПГНС?

а) Бросается монета. А – появление герба; В – появление цифры. (Да).

б) Бросают две монеты. А – появление двух гербов; В – появление двух цифр. (Нет).

в) Два выстрела по мишени. А – ни одного попадания; В – одно попадание; С – два попадания. (Нет).

Г) Два выстрела по мишени. А – хотя бы одно попадание; В – хотя бы один промах. (Нет).

Для перечисленных опытов сформируйте ПГНС.

Определить вероятность того, что партия в 100 изделий, среди которых 5 бракованных, будет поринята при проверке, если условиями приёмки допускается не более одного бракованного изделия из 50 пороверенных?

А – бракованных не оказалось среди 50 отобранных; В – одно бракованное изделие среди 50 отобранных.

3.4 В двух ящиках находятся детали: в первом – 10 деталей, из них – 3 стандартных; во втором – 15 деталей, из них – 6 стандартных. Из каждого ящика наудачу вынимают по одной детали. Найти вероятность того, что обе детали окажутся стандартными. (Р(АВ)=Р(А)Р(В)=0,12.)

3.5 Два стрелка сделали по одному выстрелу в мишень. Вероятность попадания для первого стрелка для второго -Найти: 1) вероятность того, что оба – попадут; 2) вероятность того, что оба – промахнутся;

3) вероятность того, что в мишени будет одна пробоина; 4) вероятность того, что мишень будет поражена. ( 1) 0,42; 2) 0,12; 3) 0,46; 4) 0,88.)

3.5 Электромагнитное реле типа РЭС – 100 состоит из 3-х основных узлов: катушки, якоря и контактов. Каждый из них, независимо друг от друга, может выйти из строя в течение времени T. Отказ хотябы одного узла приводит к выходу из строя всего прибора. Надёжность катушки якоря -контактов - Найти надёжность прибора в целом. (Р = 0,684.)

3.6 Электрическая цепь между точками А и В составлена по схеме:

Различные элементы цепи выходят из строя независимо одно от другого. Вероятность выхода из строя за время Т элементов цепи следующие:

элемент
вероятность	0,6	0,5	0,4	0,7	0,9

Определить вероятность перерыва в питании за указанный промежуток времени. (

Студентам, вышедшим на практику, предоставлено: 15 мест в Керчьрыбпроме, 10 – в Севастополе и 5 – на переправе. Какова вероятность того, что три друга попадут: а) на переправу ; б) в одно место.

( а) б)

Из зенитного орудия производится три выстрела по снижающемуся самолёту. Вероятность попадания при первом, втором и третьем выстрелах соответственно равны 0,1; 0,2; 0,4. Определить вероятность не менее двух попаданий. (Р = 0,124).

Происходит бой между истребителем и бомбардировщиком. Стрельбу начинает истребитель, и с вероятностью 0,2 сбивает бомбардировщик. Если после этого Б не сбит, то он открывает ответный огонь и сбивает И с вероятностью 0,3. Если И не сбит, то он снова открывает огонь и уничтожает Б с веороятностью 0,4. далее бой не продолжается. Найти вероятность того, что: а) будет сбит истребитель; б) будет сбит бомбардировщик; в) сбит хотя бы один самолёт. ( а) б) 0,2 + (1- 0,3)0,4- в) 0,24 + 0,424 = 0,664.)

3.10 На промысле в Норвежском море траулер засаливает 70% всего улова скумбрии, из них – 84% первым сортом. Какую часть улова, сдаваемого траулером на базу, будет составлять скумбрия первого сорта? (Р = 0,588.)

3.11 Три подводных охотника одновременно выстрелили в акулу. Найти вероятность того, что акула будет загарпунена, при условии, что вероятность попадания каждого охотника равна 0,6. ( Р =

3.12 Улов из 500 рыб подвергают выборочному контролю. Весь улов считается не пригодным, если из пяти прверенных рыб хотя бы одна окажется бракованной. Какова вероятность того, что данный улов не будет принят, если он содержит 5% недобракачественной рыбы?

3.13 Вероятность появления события при одном испытании равна 0,01. Сколько нужно сделать испытаний, чтобы событие произошло: а) хотя бы один раз? б) с вероятностью не меньшей 0,5? в) с вероятностью, не меньшей 0,9? ( а) 0,1 = 1 – 0,99ⁿ n > 12; б) 0,5 = 1 – (1 – 0,01)ⁿ в) 0,9 = 0,99ⁿ)

3.13 Транзистор может принадлежать к одной из трёх партий с вероятностями 0,25; 0,5; 0,25. Вероятности того, что транзистор проработает указанное число часов для этих партий, равны: 0,1; 0,2; 0,4. определить вероятность того, что транзистор проработает заданное число часов.

3.14 В ящике лежит 20 тенисных мячей, в том числе 12 – новых и 8 - игранных. Из ящика извлекают наугад 2 мяча для игры и после игры возвращают в ящик. После этого из ящика вынимают 2 мяча для следующей игры. Найти вероятность того, что эти два мяча будут неигранными.

Решение.

Гипотеза H₁ – для первой игры взяты два новых мяча;

P(H₁) =

Гипотеза Н₂ – для первой игры взяли один новый, один старый мяч;

Р(Н₂) =

Гипотеза Н₃ – для первой игры выбрали два старых мяча;

Р(Н₃) =

Событие А - для второй игры взяли два новых мяча.

Р(А/H₁) = р(А/H₂) = Р(А/Н₃) =

Р(А) = Р(Н₁)Р(А/Н₁) + Р(Н₂)Р(А/Н₂) +Р(Н₃)Р(А/H₃) = 0,279.

3.15 По террористу, устанавливающему взрывное устройство, производят два одиночных выстрела из снайперской винтовки с корректировкой стрельбы. Вероятность попадания при первом выстреле, когда он стоит на коленях согнувшись, равна 0,7. При втором, когда после первого выстрела он поднялся на ноги – 0,8. В случае промаха до третьего выстрела он успевает скрыться. Для обезвреживания террориста достаточно двух попаданий. При одном попадании он может быть убит с вероятностью 0,6. Найти вероятность того, что в результате двух выстрелов террорист будет убит.

Решение.

Гипотеза Н₁ – одно попадагние при двух выстрелах;

Р(Н₁) =

Гипотеза Н₂ – два попадания при двух выстрелах;

Р(Н₂) =

Вероятность обезвредить при одном попадании: Р(У/Н₁) = 0,6;

Вероятность обезвредить при двух попаданиях: Р(У/Н₂) = 1;

Р(У) = Р(Н₁)Р(У/Н₁) + Р(Н₂)Р(У/Н₂) = 0,788.

3.16 Имеется две партии однородных изделий. Первая партия состоит из 30 изделий, среди которых 2 дефектных. Вторая партия состоит из 40 изделий, среди которых – 5 дефектных. Из первой партии случайным образом берутся 15 изделий, а из второй – 25. Эти изделия смешиваются и образуется новая партия, из которой наугад берётся одно изделие. Найти вероятность того, что изделие будет дефектным.

Решение.

Составим ряд распределения для дефектных деталей по первой партии:

Мода (наиболее вероятное число дефектных деталей, взятых из первой партии), равна: деталь

Наиболее вероятное число дефектных деталей, извлечённых из второй партии, равно: детали. ()

Таким образом, во вновь образованной партии из 40 деталей будет 4 дефектных детали. Вероятность выбрать из неё одну дефектную деталь составляет

3.17 При отклонении от нормального режима работы автомата срабатывает сигнализатор С -1 с вероятностью 0,8; а сигнализатор С – 2 с вероятностью 1. Вероятность того, что автомат снабжён сигнализатором С – 1 или С – 2 соответственно равны 0,6 и 0,4. Получен сигнал о разладке автомата. Каким сигнализатором снабжён автомат, С – 1 или С – 2?

Решение.

Гипотеза Н₁ – автомат снабжён сигнализатором С – 1, Р(Н₁) = 0,6;

Гипотеза Н₂ – автомат снабжён сигнализатором С – 2, Р(Н₂) = 0,4;

Вероятность срабатывания автомата с сигнализатором С – 1 равна Р(А/Н₁) = 0,8. Вероятность срабатывания с сигнализатором С – 2 равна Р(А/Н₂)=1.

Вероятность срабатывания в случае разладки с любым сигнализатором равна: Р(А) = Р(Н₁)Р(А/Н₁) + Р(Н₂)Р(А/Н₂)=

Вероятность срабатфывания первого сигнализатора при разладке равна:

Р(Н₁/А) = Второго – Р(Н₂/A) = 0,455.

Автомат снабжён первым сигнализатором.

3.18 Партия состоит из вентиляторов рижского и московского заводов. В партии 70% вентиляторов рижского завода. Надёжность вентилятора московского завода за время t равна 0,95; рижского – 0,92. Прибор за время t работал безотказно. Найти вероятность того, что испытывался вентилятор московского завода.

Гипотеза Н₁ – на испытание взят вентилятор рижского завода, Р(Н₁) = 0,7.

Гипотеза Н₂ – на испытание попал московский вентилятор. Р(Н₂) = 0,3.

Вероятность надёжной работы с вентилятором из Риги Р(А/Н₁) = 0,92, а с вентилятором из Москвы – Р(А/Н₂) = 0,95.

Вероятность безотказной работы с любым вентилятором равна:

Р(А) = Вероятность того, что испытывался московский вентилятор, равна: Р(Н₂/А) =

3.19 Два стрелка сделали по выстрелу в мишень. Вероятность попадания первым – Р₁ = 0,6; Для второго – Р₂ = 0,7. Какова вероятность: а) двух попаданий; б) двух промахов; в) одного попадания; г) вероятность поражения мишени.

( а) 0,42; б) 0,12; в) 0,46; г) 0,88.)

4. Случайные величины, законы распределения, числовые характеристики

случайных величин.

4.1 По пуути движения автомашины 4 светофора. Каждый из них с вероятностью 0,5 либо разрешает (р), либо запрещает (q) проезд. Построить ряд распределения, многоугольник распределения и функцию распределения вероятностей числа светофоров, пройденных машиной без остановки. Найти математическое ожидание, дисперсию, моду распределения.

Решение.

Обозначим случайную величину – число пройденных без остановки светофоров символом Х. Её возможные значения: 0; 1; 2; 3; 4. Ряд распределения:

хi
Р(хi)=рi	q=0,5	Pq=0,25	P2q=0,125	P3q=0,0625	P4 =0,0625

Мат. ожидание: М(Х) = ед. с. в.

Дисперсия: D(X)=ед².

Мода: М₀ = 0.

4.2 Из партии в 25 изделий, среди которых имеется 6 нестандартных, случайным образом выбраны для проверки их качества 3 изделия. Составить ряд распределения случайной величины Х – числа нестандартных изделий, содержащихся в выборке.

()

хi
pi	0,41	0,43	0,11	0,05

4.3 Предполагая одинаковыми вероятности рождения мальчика и денвочки, составить закон распределения случайной величины Х, котораявыражает число мальчиков в семье, имеющей 5 детей.

( Закон распределения с. в. Х – биномиальный. )

xi
pi	0,03125	0,15625	0.3125	0,3125	0,15625	0,03125

 

4.4 На отрезке дана функция вне его функция равна нулю. При каком к функция будет плотностью распределения вероятностей некоторой случайной величины X? Найти функцию распределения F(x). Определить вероятность того, что с. в. Х примет значение, не меньше (-1), но не больше 1.

Решение.

4.5 Дано: Определить: а) может ли эта функция быть плотностью вероятности некоторой случайной величины; б) вероятность того, что случайная величина примет свои значения из промежутка ; в) вероятность того, что в трёх независимых испытаниях она два раза окажется в указанном промежутке. ( а) Да. б) р = 2/27. в) р = 0,142.)

4.6 Случайная величина задана функцией распределения.

 

Требуется: а) найти плотность распределения вероятностей; б) определить вероятность того, что в результате испытания случайная величина примет значения, принадлежащие промежутку .

Решение.

а) б)

4.7 Функция распределения случайной величины Т – времени безотказной работы холодильной установки имеет вид:

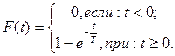
Найти: а) плотность вероятности f(t); б) вероятность безотказной работы аппаратуры в течение времени Т.

Решение.

а) 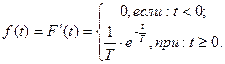б)

4.8 Случайная величина Х задана функцией распределения:

Найти вероятность того, что в результате трёх независимых испытаний с. в. Х ровно 2 раза примет значения, принадлежащие промежутку .

(р = 27/64.)

4.9 Вероятность изготовления стандартной детали равна 0,9. Какова вероятность того, что среди 5 деталей не более одной настандартной?

( Биномиальное распределение, p=0,1;q=0,9.)

4.10 При движении по поросёлочной дороге автомобиль испытывает в среднем 60 толчков в течение часа. Какова вероятносать того, что за 30 секунд не будет ни одного толчка?

Решение.

Минутная интенсивность толчков дороги равна

Закон распределения – пуассоновский.

 

5.Задачи на законы распределения дискретных и непрерывныъх случайных ве - личин.

5.1 В мастерской имеется 4 мотора. При существующем режиме работы вероятность того, что мотор работает с полной нагрузкой, равна 0,8. найти вероятность того, что в данный момент не менее двух моторов работает с полной нагрузкой. ( )

5.2 На автобазе имеется 12 автомашин. Вероятность выхода на линию каждой из них равна 0,8. найти вероятность нормальной работы автобазы, если для этого необходимо иметь на линии не менее 8 автомашин.

5.3 Вероятность возникновения опасной для прибора перегрузки в каждом опыте равна 0,4. Определить вероятность отказа прибора в серии из 3-х независимых опытов, если вероятность отказа прибора при одной, двух и трёх опасных перегрузках соответственно равны 0,2; 0,5; 0,8.

Решение.

Определим вероятности одной, двух и трёх опасных перегрузок в серии из трёх опытов (вероятности гипотез Н₁, Н₂, Н₃ соответственно).

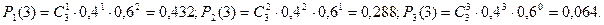
Вероятность отказа (событие А) находим по формуле полной вероятности:

5.4 Ожидается прибытие трёх судов с бананами. Статистика показывает, что в 1% случаев груз бананов портится в дороге. Составить ряд распределения, найти мат. ожидание и дисперсию числа судов с испорченным грузом.

Решение.

Случайная величина Х – число судов с испорченным грузом, её возможные значения равны: 0; 1; 2; 3. Подсчитаем вероятности этих значений. Закон распределения – биномиальный, с параметрами: р = 0,01; q = 0,99.

М(Х) = np = 0,03; D(X) = npq = 0,0297.

5.5 Рабочий обслуживает 4 станка. Каждый станок в течение 6 часов работы несколько раз останавливается, и всего в сумме простаивает 0,5 часа, причём, остановки станков в любой момент времени равновероятны. Составить ряд распределения числа станков, работающих в данный момент времени. Найти числовые характеристики.

Решение.

Случайная величина Х – число станков, работающих в данный момент времени. Её возможные значения: 0; 1; 2; 3; 4. Каждый станок пребывает в двух состояниях: рабочем, вероятность такого состояния р равна отношению временного промежутка, когда он работает, к всему рабочему времени р= 5,5час/6час= 11/12; нерабочем, вероятность этого состояния q = 0,5час./6час.=1/12.

Ряд распределения для с. в. Х имеет вид:

хi
P(xi)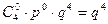

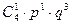
Закон распределения с. в. Х – биномиальный, поэтому числовые характеристики вычисляем по формулам:

5.6 При массовом производстве полупроводниковых диодов вероятность брака при формовке равна 0.1. Какова вероятность того, что из 400 взятых наугад диодов 50 будут бракованными? (n=400; p=0,1; q=0,9; m=50).

5.7 При проверке контродьных работ, выполненных студентами по определённой теме, было выявлено, что только 60% студентов из числа писавших контрольную работу, смогли правильно ответить на все поставленные вопросы.

Найти вероятность того, что из 100 случайно взятых контрольных работ 60 из них написаны студентами, сумевшими правильно ответить на все поставленные вопросы.

5.8 Вероятность выхода из строя за время Т одного конденсатора рапвна 0,2. определить вероятность того, что из 100 конденсаторов в течение времени Т выйдет из строя не менее 30 конденсаторов.

P = 0,2; q = 0,8; m30; n = 100.

5.9 Вероятность загорания леса от удара молнии во время отдельной грозы равна 0,1. За лето над лесом возникает в среднем 360 гроз. а) Какова вероятность возникновения от 30 до 50 очагов пожара? б) Каково наивероятнейшее число возникающих от гроз очагов возгорания и какова его вероятность?

P = 0,1; q = 0,9; n = 360; ;

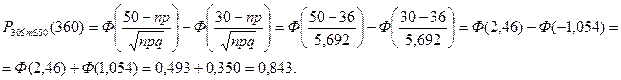
М₀ = 36 – наивероятнейшее число возникающих очагов возгорания.

5.10 Среднее число вызовов, поступающих в справочное бюро вокзала за одну минуту, равно двум. Найти вероятность того, за три минуты поступит: а) четыре вызова; б) менее четырёх вызовов; в) не менее четырёх вызовов.

Решение.

Минутная плотность вызовов равн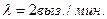а а)

б)

в)

5.11 Случайная величина имеет плотность Найти постоянную а и вероятность того, что в двух независимых испытаниях Х примет значения, меньше единицы.

Решение.

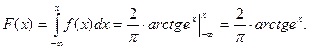
5.12 Случайная величина распределена по закону Релея:

Найти коэффициент А, медиану, моду, М(Х), D(X).

(А=2h²; М(Х)= )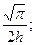

5.13 Заряд охотничьего пороха взвешивают на весах, имеющих мг. Номинальный вес заряда равен 2,3 г. Определить вероятность разрыва ружья, если максимально допустимый заряд равен 2,5 г.

Решение.

Случайная величина Х – вес порохового заряда. Закон распределения вероятностей – нормальный. Разрыв произойдёт, если вес заряда превысит 2,5 г.

=

5.14 Систематическая ошибка дальномера равна +20 метров, а случайные ошибки распределены по нормальному закону. Какое с.к.о. должен иметь дальномер, чтобы с вероятностью 0,9 ошибка измерения высоты по абсолютной величине не превышала 100 м?

Решение.

Случайная величина Х – ошибка в измерении расстояния до цели, по абсолютной величине не должна превышать 100 м.

P(-100 < M(X) <100) = F(100) – F(-100), здесь М(Х) =0 – точное расстояние до цели. Тогда:

F(100) – F(-100) = метров.

5.15 Перед руйсом длиной в 3000 миль все форсунки главного двигателя (их 8 штук) заменили новыми. Продолжительность работы одной форсунки до отказа – случайная величина Т, подчинённая нормальному закону со средним временем безотказной работы 5000 миль и с.к.о. =1000 миль. Какова вероятноть того, что ни одна форсунка не откажет в рейсе?

Решение.

Закон распределения с. в. Т – нормальный, усечённый на 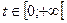. Нормирующий множитель при этом получает значение:

Тогда вероятность безотказной работы одной форсунки за рейс длиной в 3000 миль можно подсчитать по формуле:

Вероятность того, что все 8 форсунок не откажут в рейсе (вероятность произведения 8-ми независимых событий с одинаковой вероятностью появления), подсчитается по формуле: