Группировочные данные по торговой площади магазинов

 

Торговая площадь магазинов, кв. м	Число магазинов, единиц
До 100 От 100 до 120 От 120 до 140 От 140 до 160 От 160 до 180 Свыше 180
ИТОГО

 

Как видно из сгруппированных данных, модальный интервал будет лежать в границах интервала от 140 до 160 кв. м, так как этому интервалу соответствует большая частота (20 магазинов).

Теперь подставим числовое значение из приведенного примера в формулу

 

Следовательно, из этой группы больше всего магазинов имеют торговую площадь 141,5 кв. м.

Как и мода, медиана относится к структурным средним, она так же является конкретной величиной. Размеры отклонений значе­ний других вариант на моду и медиану не оказывают влияния.

Медианой называется серединная варианта упорядоченно­го вариационного ряда, расположенного в возрастающем и убы­вающем порядке. Она является центральным членом и делит ва­риационный ряд пополам в тех случаях, если этот ряд нечетный.

В ряду, состоящем из 15 чисел, медианой будет 8-е число, от которого как вниз, так и вверх будет расположено по 7 чисел.

Например, в торговле эти две величины применяются при определении покупательского спроса на отдельные продовольственные и непродовольственные товары, при определении качества товаров и т.д.

Пример.

А. Дан нечетный вариационный ряд роста студенток

156 158 160 166 168 172

Из приведенного нечетного ряда видно, что центральным членом (медианой) данного ряда является рост студентки — 161 см.

В случае четного вариационного ряда медиана определяется следующим образом: серединные два члена вариационного ряда складываются и делятся пополам.

Б. Дан четный вариационный ряд роста студенток

155 156 158 160 161 166 168 172

 

Расчет медианы интервального ряда.

Если варианты в ряду распределения заданы в виде интервалов, то первоначально находят медианный интервал, который содержит единицу, находящуюся в середине ранжированного ряда. Для опре­деления этого интервала сумму частот делят пополам и на основе последовательного суммирования частот первого, второго, третьего и т.д. интервалов находят интервал, где расположена медиана. При­ближенное значение М_е в медианном интервале исчисляется по фор­муле:

 

где х₀ — нижняя граница медианного интервала;

i — величина медианного интервала;

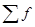— сумма частот интервального ряда;

S_(m-1) — сумма накопленных частот в интервалах предшест­вующих медианному;

f_m — частота медианного интервала.

Из этой формулы следует, что к нижней границе медианного интервала (х₀) добавляется та часть медианного интервала, которая пропорциональна удельному весу в частоте медианного интервала части ее, расположенной от нижней границы интервала до М_е.

Пример. В интервальном ряду (табл. 5.9) даны группы семей по среднемесячному доходу на 1 человека. Требуется определить для этого ряда серединное значение, т.е. медиану.

 

Таблица 5.9