Основные типы уравнений математической физики

 

 

Основными уравнениями математической физики (для случая функций двух независимых переменных) считаются следующие дифференциальные уравнения в частных производных второго порядка.

І. В о л н о в о е у р а в н е н и е :

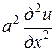. (1)

 

К исследованию этого уравнения приводит рассмотрение процессов поперечных колебаний струны, продольных колебаний стержня, электрических колебаний в проводе, крутильных колебаний вала, колебаний газа и т.д. Это уравнение является простейшим уравнением гиперболического типа.

ІІ. У р а в н е н и е т е п л о п р о в о д н о с т и ( у р а в н е н и е Ф у р ь е ) :

 

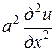. (2)

 

К исследованию этого уравнения приводит рассмотрение процессов распространения тепла, фильтрации жидкости и газа в пористой среде, некоторые вопросы теории вероятностей и т.д. Это уравнение является простейшим уравнением параболического типа.

ІІІ. У р а в н е н и е Л а п л а с а :

 

. (3)

 

К исследованию этого уравнения приводит рассмотрение задач об электрических и магнитных полях, о стационарном тепловом состоянии, задач гидродинамики, диффузии и т.д. Это уравнение является простейшим уравнением эллиптического типа.

В уравнениях (1), (2) и (3) искомая функция и зависит от двух переменных. Рассматриваются также соответствующие уравнения и для функций с большим числом переменных. Так, например, волновое уравнение с тремя независимыми переменными имеет вид

 

,

 

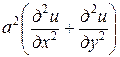уравнение теплопроводности с тремя независимыми переменными имеет вид

 

,

 

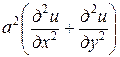уравнение Лапласа с тремя независимыми переменными имеет вид

 

.
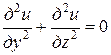