Закон дробления оболочки на осколки

Закон дробления устанавливает распределение осколков по величине их масс. Он может быть получен, в основном, экспе­риментальным путем и носит статистический характер. Послед­нее объясняется тем, что характер дробления сплошной оболоч­ки в каждом конкретном случае зависит от множества различ­ных факторов, в том числе и от тех, которые носят случайный характер. Поэтому, чтобы учесть эти случайности, получить надежные оценки параметров и выявить вполне определенные закономерности, свойственные БЧ рассматриваемого типа, не­обходимо произвести достаточно большое число опытов и обра­ботку их результатов статистическими методами

Суть экспериментов состоит в подрыве боевых частей или их макетов в специальных ямах или бронекамерах, заполнен­ных песком, опилками или другими улавливателями осколков. Материал улавливателей не должен приводить к разрушению попадающих в него осколков и не вносить тем самым погреш­ностей в результаты экспериментов. Собранные после подры­ва БЧ осколки взвешиваются и сортируются по интервалам масс на всей непрерывной шкале от минимального до мак­симального значения. Далее находятся как общее количе­ство осколков , так и количество осколков , приходя­щихся на интервал масс

(

Минимальная масса осколка зависит от массы БЧ. Обыч­но принимают равной 0,5 г или 1 г, так как осколки меньшей массы могут быть недостаточно эффективными. Для сверхмалых калибров БЧ может быть меньше 0,5 г, однако эти ос­колки технически трудно собрать и отделить от фракций разру­шенного улавливателя.

Собранные осколки в сумме образуют массу осколков 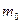, которая, естественно, всегда меньше массы металла оболоч­ки , то есть всегда имеет место соотношение

, (9.2)

где <1 - коэффициент, учитывающий реализацию металла оболочки.

. Коэффициент зависит от механических свойств металла. Например, для оболочек из стали <0,9. У оболочек из ков­кого чугуна уменьшается до 0,64, а у оболочек из сталистого чугуна - до 0,48.

Как уже отмечалось, величины и носят статисти­ческий характер и при осуществлении нескольких подрывов БЧ должны быть определены как средние значения по всем экспериментам.

Отношение представляет собой статистическую ве­роятность того, что любой взятый наугад осколок будет прихо­диться на интервал масс заключенный в промежутке от до . Отношение статистической вероятности к соответ­ствующему интервалу масс дает возможность найти высоту столбца

(9.3)

Определив для можно построить гис­тограмму распределения. Примерный вид гистограммы приведен на рисунке 5.5. На этом же рисунке приведена сглажи­вающая кривая , которую принято называть дифференци­альным законом распределения осколков по величине масс. Гистограмма и сглаживающая кривая должны удовлетворять следующим очевидным свойствам:

Заметим также, что площадь каждого столбца гистограммы (на рисунке 9.5 она обозначена штриховкой) численно равна отно­сительному количеству осколков, приходящихся на данный ин­тервал масс.

Иногда удобно представлять экспериментальные данные по распределению масс осколков в виде гистограммы, имеющей смысл статистического интегрального закона распределения определяемого выражением

(9.4)

 

Рисунок 9.5. Гистограмма и дифференциальный закон

распределения осколков по ве­личине масс .

 

Рисунок . 9.6. Гистограмма и интегральный закон

) распре­деления осколков по величине масс

На рисунке 9.6 приведены примерный вид этой гистограммы, а также сглаживающая кривая , которую называют интег­ральным законом распределения масс осколков. Зависимости и должны быть неубывающими функциями своих аргументов и удовлетворять следующим основным свойствам:

;

Разность соседних столбцов и численно равна относительному количеству осколков, приходящихся на рассматриваемый интервал массы. Кроме того, законы распре­деления /(<7) и связаны между собой следующим соотно­шением:

(9.5)

Наличие гистограмм и соответствующих сглаживающих кривых позволяет решать следующие задачи:

- находить количество осколков или , мас­са которых меньше или больше заданного значения ;

- рассчитывать количество осколков , масса которых заключена в интервале ;

- определять среднюю массу осколка .

В соответствии с выражениями (5.3) и (5.4) для соответствующих гистограмм, находим:

(9.6)

(9.7)

(9.8)

(9.9)

Аналогичные зависимости могут быть получены при наличии кривых и .

Формулы (9.6) ... (9.9) являются расчетными и позволяют решать многие практические задачи, связанные с оценкой эф­фективности поражающего действия боевых частей осколочного типа и безопасностью их боевого применения.

Исследования процесса дробления оболочек различных БЧ, отличающихся конструктивными параметрами и технологией изготовления, позволяют установить некоторые общие законо­мерности процесса дробления. Так было обнаружено, что при нерегулярном дроблении оболочек в процессе взрыва БЧ обра­зуется всегда больше осколков меньшей массы, поэтому кривые и по внешнему виду очень близки к степенным функ­циям. При полурегулярном дроблении характер изменения кри­вых сохраняется, однако интервал допустимых значений их аргументов сужается (рисунок 9.7, а).

 

Рисунок 9.7. Законы распределения осколков по величине масс:

а - при полурегулярном и б - регулярном дроблении корпусов на

осколки

В пределе, то есть при полном регулярном дроблении корпусов на осколки заданной мас­сы , законы и превращаются соответственно в 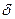-функцию и ступенчатую функцию соответственно (рисунок 9.7,б). Устойчивость характера изменения законов и по­зволила установить следующую закономерность - найти доста­точно общие законы и безразмерной величины , представляющей собой относительную массу осколка

(9.10)

изменяющуюся в диапазоне

Проф. Р.С.Саркисяном путем обработки многочисленных экспериментальных данных было найдено следующее выраже­ние для аппроксимации закона :

, (9.11)

в котором , и - постоянные коэффициенты. Параметр представляет собой нормирующий множитель, определяе­мый из условия

Зная закон распределения (9.11) и массу осколка , мож­но найти закон распределения по известной из теории ве­роятностей формуле

(9.12)

Из (9.10) следует, что . Поэтому с учетом (9.11) и (9.12) находим

(9.13)

Дифференциальные законы распределения осколков по ве­личине относительных (9.11) или абсолютных (9.13) значе­ний масс описывают целый класс некоторых сходных по устройству АСП. Примером таких АСП могут служить авиа­бомбы модели М-54, которые являются одинаковыми по уст­ройству и отличаются только калибром (от 250 до 3000 кг).

Современная теория боеприпасов осколочного типа показы­вает, что при прочих равных условиях большей эффективностью обладают БЧ с дроблением корпусов на осколки компактной формы и заданной, в известном смысле оптимальной массы. Современные технологии изготовления корпусов и БЧ в целом позволяют решить эту задачу относительно просто. Одним из первых способов полурегулярного дробления корпусов был предложен профессором

Г. И. Покровским, который обосновал пилообразный профиль внутренней поверхности литого корпуса осколочных и осколочно-фугасных авиабомб (рисунок. 9.8, а). В процессе взрыва заряда и расширения корпусов их разруше­ние начинается в местах с минимальной толщиной стенок , вследствие чего корпус как бы разрывается на отдельные коль­ца. В дальнейшем дробление отдельных колец происходит слу­чайным образом. Такой способ организации дробления исключа­ет образование осколков слишком большой массы и некомпа­ктной формы.

Аналогичным образом идет процесс формирования осколков корпусов БЧ, набранных из отдельных заранее изготовленных колеи или представляющих собой пруток прямоугольного сечения, навитый на металлический стакан в виде пружины (рисунок 9.8, б). К способам полурегулярного дробления корпу­сов следует отнести также использование пластмассовых «рубашек» с кумулятивными выемками (рисунок 9.8, в).

Рисунок. 9.8. Способы полурегулярного дробления

корпусов на осколки

Рубашки в процессе изготовления зарядов заполняются ВВ. При детонации заряда в выемках рубашки формируется газовая кумулятивная струя, создающая повышенные концентрации напряжений на поверхности примыкающего к ней металлического корпуса, что и обеспечивает образование осколков примерно одинаковой массы. Примерно таким же способом обеспечивается формиро­вание осколков с относительно небольшим разбросом масс, когда корпус предварительно обрабатывается лазерным лучом, создающим в узких «щелях» микроструктуру металла с более низкими прочностными свойствами (рисунок 9.8,г).

Регулярное дробление корпусов на осколки одинаковой массы и формы может быть обеспечено путем формирования на одной или обеих поверхностях стенок корпуса глубоких вы­точек (канавок), которые заметно ослабляют прочность стенок по указанным сечениям (рисунок. 9.9, а). Наиболее совершенный способ регулярного дробления корпусов БЧ достигается в том случае, когда их стенки представляют собой наборы из зара­нее изготовленных осколков заданной массы и формы (рисунки 9.9,6, г). Однако необходимо иметь в виду, что в этом случае при взрыве заряда практически сразу же нарушается сплошность корпуса.

 

Рисунок 9.9. Способы регулярного дробления корпусов на осколки

 

В образовавшиеся между осколками зазоры начинается интенсивное истечение ПД, вследствие чего сами осколки могут заметно оплавляться, а их начальная ско­рость при этом весьма существенно уменьшается.