Обработка результатов многократных измерений
Диапазон измерительных величин и их количество постоянно растут, и поэтому возрастает и сложность измерений. Они перестают быть однократным действием и превращаются в сложную процедуру подготовки и проведения измерительного эксперимента и обработки полученной информации.
Другой причиной важности измерений является их значимость. Основа любой формы управления, анализа, прогнозирования, контроля или регулирования – достоверная исходная информация, которая может быть получена лишь путем измерения требуемых физических величин, параметров и показателей. Только высокая и гарантированная точность результатов измерений обеспечивает правильность принимаемых решений.
Поэтому в случае, когда случайная составляющая погрешности однократного измерения может превысить требуемые по условиям задачи значение, выполняют ряд последовательных отдельных измерений и получают одно многократное измерение, погрешность которого может быть уменьшена методами математической статистики.
Многократным называют измерение физической величины одного размера, результат которого получен из нескольких следующих друг за другом измерений, то есть состоящее из ряда однократных измерений.
Из опыта известно, что ни одно измерение, как бы тщательно оно не проводилось, не может дать абсолютно точный результат, вследствие чего часто говорят о наличии ошибок и погрешностей при проведении измерительного эксперимента. Всегда существует множество факторов, в том числе и случайных, приводящих к искажениям получаемой измерительной информации.
При условии исключения из результатов экспериментов систематических и грубых ошибок, остается лишь случайная составляющая погрешности. Случайную ошибку можно рассматривать как суммарный эффект действия многих факторов, каждый из которых не проявляет себя отчетливо. Поэтому случайные ошибки при многократных измерениях получаются различными как по величине, так и по знаку. Их невозможно учесть как систематические, но можно учесть их влияние на оценку истинного значения измеряемой величины. Анализ случайных ошибок является важнейшим разделом математической обработки экспериментальных данных.
Для получения результатов, минимально отличающихся от истинных значений величин, проводят многократные наблюдения за измеряемой величиной с последующей математической обработкой опытных данных. Поэтому наибольшее значение имеет изучение погрешности как функции номера наблюдения, т.е. времени ∆(t). Тогда отдельные значения погрешностей можно будет трактовать как набор значений этой функции:
∆1= ∆(t1), ∆2= ∆(t2),… ∆n= ∆(tn).
В общем случае погрешность является случайной функцией времени, которая отличается от классических функций математического анализа тем, что нельзя сказать, какое значение она примет в момент времени t. Можно указать лишь вероятности появления ее значений в том или ином интервале.
При проведении измерений целью является оценка истинного значения измеряемой величины, которое до опыта неизвестно. Результат измерения включает в себя помимо истинного значения еще и случайную погрешность, следовательно, сам является случайной величиной. В этих условиях фактическое значение случайной погрешности, полученное при поверке, еще не характеризует точности измерений, поэтому не ясно, какое же значение принять за окончательный результат измерения и как охарактеризовать его точность.
Ответ на эти вопросы можно получить, используя при метрологической обработке результатов измерения методы математической статистики, имеющей дело именно со случайными величинами.
Рассмотрим результат наблюдений х за постоянной физической величиной Q как случайную величину, принимающую различные значения Z, в различных наблюдениях за ней. Значения Xi будем называть результатами отдельных наблюдений.
Наиболее универсальный способ описания случайных величин заключается в отыскании их интегральных или дифференциальных функций распределения.
Под интегральной функцией распределения результатов наблюдений понимается зависимость вероятности того, что результат наблюдения Xi в i–м опыте окажется меньшим некоторого текущего значения х, от самой величины х:
Здесь и в дальнейшем большие буквы используются для обозначения случайных величин, а маленькие – значений, принимаемых случайными величинами.
Более наглядным является описание свойств результатов наблюдений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей:
Физический смысл f(x) состоит в том, что произведение f(x)dx представляет вероятность попадания случайной величины Х в интервал от х до х+dx , т.е.
Свойства плотности распределения вероятности:
― 
– вероятность достоверного события равна 1; иными словами, площадь, заключенная между кривой дифференциальной функции распределения и осью абсцисс, равна единице;
― 
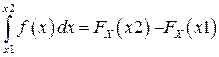– вероятность попадания случайной величины в интервал от х1 до х2.
От дифференциальной функции распределения легко перейти к интегральной путем интегрирования:
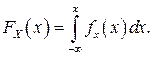
Размерность плотности распределения вероятностей обратна размерности измеряемой величины, поскольку сама вероятность – величина безразмерная.
Таким образом, вероятность попадания результата наблюдения или случайной погрешности в заданный полуоткрытый интервал равна площади, ограниченной кривой распределения, осью абсцисс и перпендикулярами к ней на границах этого интервала. Необходимо отметить, что результаты наблюдений в значительной степени сконцентрированы вокруг истинного значения измеряемой величины и по мере приближения к нему элементы вероятности их появления возрастают. Это дает основание принять за оценку истинного значения измеряемой величины координату центра тяжести фигуры, образованной осью абсцисс и кривой распределения, и называемую математическим ожиданием результатов наблюдений:
Функция распределения является самым универсальным способом описания поведения случайных погрешностей. Однако для определения функций распределения необходимо проведение весьма кропотливых научных исследований и обширных вычислительных работ. Поэтому к такому способу описания случайных погрешностей прибегают иногда при исследовании принципиально новых мер и измерительных приборов.
Значительно чаще бывает достаточно охарактеризовать случайные погрешности с помощью ограниченного числа специальных величин, называемых моментами [3].
Начальным моментом n–го порядка результатов наблюдений называется интеграл вида
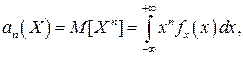
представляющий собой математическое ожидание степени Хn.
При n=1
т.е. первый начальный момент совпадает с математическим ожиданием результатов измерений.
Центральным моментом n–го порядка результатов наблюдений называется интеграл вида
Вычислим первый центральный момент:
Таким образом, первый центральный момент результатов наблюдений равен нулю. Важно отметить, что начальные и центральные моменты случайных погрешностей совпадают между собой и с центральными моментами результатов наблюдений, поскольку математическое ожидание случайных погрешностей равно нулю.
Особое значение наряду с математическим ожиданием результатов наблюдений имеет второй центральный момент, называемый дисперсией результатов наблюдений.
При n=2
Дисперсия D[X] случайной погрешности равна дисперсии результатов наблюдений и является характеристикой их рассеивания относительно математического ожидания.
Если математическое ожидание результатов наблюдений можно рассматривать в механической интерпретации как абсциссу центра тяжести фигуры, заключенной между кривой распределения и осью Ох, то дисперсия является аналогом момента инерции этой фигуры относительно вертикальной оси, проходящей через центр тяжести.
Дисперсия имеет размерность квадрата измеряемой величины, поэтому она не совсем удобна в качестве характеристики рассеивания. Значительно чаще в качестве последней используется положительное значение корня квадратного из дисперсии, называемое средним квадратическим отклонением результатов наблюдений:
С помощью среднеквадратического отклонения можно оценить вероятность того, что при однократном наблюдении случайная погрешность по абсолютной величине не превзойдет некоторой наперед заданной величины ε, т.е. вероятность P{|δ|}< ε. Для этого рассмотрим формулу, известную как неравенство Чебышева:
или
.
Полагая ε = 3σх, можно найти вероятность того, что результат однократного наблюдения отличается от истинного значения на величину, большую утроенного среднеквадратического отклонения, т. е. вероятность того, что случайная погрешность окажется больше 3σх:
Вероятность того, что погрешность измерения не превысит 3σх, составит соответственно P{|δ|}< ε ≥1 – 0,11=0,89.
Неравенство Чебышева дает только нижнюю границу для вероятности P{|δ|}< ε, меньше которой она не может быть ни при каком распределении. Обычно P{|δ|}< ε значительно больше 0,89. Так, например, в случае нормального распределения погрешностей эта вероятность составляет 0,9973.
Математическое ожидание и дисперсия являются наиболее часто применяемыми моментами, поскольку они определяют наиболее важные черты распределения: положение центра распределения и степень его разбросанности. Для более подробного описания распределения используются моменты более высоких порядков.
Третий момент случайных погрешностей служит характеристикой асимметрии, или скошенности распределения. В общем случае любой нечетный момент случайной погрешности характеризует асимметрию распределения. Отличие этих моментов от нуля как раз и указывает на асимметрию распределения. Простейшим из нечетных моментов является третий момент μ3[δ]. Чтобы получить безразмерную характеристику, третий момент делят на третью степень среднеквадратического отклонения и получают коэффициент асимметрии, или просто асимметрию Sk распределения:
Для иллюстрации сказанного на рисунке 5 приведены три кривые распределения случайных погрешностей с положительной, отрицательной и нулевой асимметрией.
Рисунок 5 – Кривые распределения случайных погрешностей с положительной, отрицательной и нулевой асимметрией
Четвертый момент служит для характеристики плосковершинности распределения случайных погрешностей. Эти свойства описываются с помощью эксцесса – безразмерной характеристики, определяемой выражением
Для нормального распределения эксцесс равен нулю, более плосковершинные распределения обладают отрицательным эксцессом, более островершинные – положительным.
Случайная погрешность измерения образуется под влиянием большого числа факторов, сопутствующих процессу измерения. В каждой конкретной ситуации работает свой механизм образования погрешности. Поэтому естественно предположить, что каждой ситуации должен соответствовать свой тип распределения погрешности. Однако во многих случаях имеются возможности еще до проведения измерений сделать некоторые предположения о форме функции распределения, так что после проведения измерений остается только определить значения некоторых параметров, входящих в выражение для предполагаемой функции распределения.
В практика измерений широкое распространение получило нормальное распределение погрешностей, что объясняется центральной предельной теоремой теории вероятностей, являющейся одной из самых замечательных математических теорем, в разработке которой принимали участие многие крупнейшие математики – Муавр, Лаплас, Гаусс, Чебышев и Ляпунов. Центральная предельная теорема утверждает, что распределение случайных погрешностей будет близко в нормальному всякий раз, когда результаты наблюдения формируются под влиянием большого числа независимо действующих факторов, каждый из которых оказывает лишь незначительное действие по сравнению с суммарным действием всех остальных.
Задача оценки истинного значения на основании полученной в эксперименте группы результатов наблюдений, т.е. нахождения результата измерений, и оценки его точности, т.е. меру его приближения к истинному значению, является частным случаем статистической задачи нахождения оценок параметров функции распределения случайной величины на основании выборки – ряда значений, принимаемых этой величиной в n независимых опытах.
Для наиболее часто встречающегося на практике нормального распределения случайных погрешностей оценки максимального правдоподобия имеются особые обозначения.
Оценкой истинного значения является среднее арифметическое из результатов отдельных наблюдений xi,
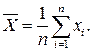
Вторая производная от логарифмической функции преобразования равна
,
поэтому дисперсия среднего арифметического в n раз меньше дисперсии σ2x результатов наблюдений, т. е.
Оценка дисперсии результатов наблюдений при малом n является немного смещенной, поэтому точечную оценку дисперсии принято определять как
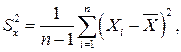
а оценку среднеквадратического отклонения результатов наблюдений как
Дисперсия оценки Sx среднеквадратического отклонения составляет
С помощью полученных оценок итог измерений можно записать в виде
что уже позволяет сделать некоторые выводы относительно точности проведенных измерений.
В настоящее время большое распространение получила оценка с помощью интервалов. Смысл оценки параметров с помощью интервалов заключается в нахождении интервалов, называемых доверительными, между границами которых с определенными вероятностями (доверительными) находятся истинные значения оцениваемых параметров.
Вначале остановимся на определении доверительного интервала для среднего арифметического значения измеряемой величины. Предположим, что распределение результатов наблюдений нормально и известна дисперсия σ2x Найдем вероятность попадания результата наблюдений в интервал (mx – tpσx, mx + tpσx). Согласно формуле для интегральной функции нормированного нормального распределения Ф(tp)
но
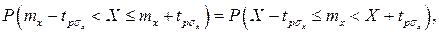
и, если систематические погрешности исключены (mx=Q),
Это означает, что истинное значение Q измеряемой величины с доверительной вероятностью P=2Ф(tp)–1 находится между границами доверительного интервала (X – tpσx, X + tpσx).
Половина длины доверительного интервала tpσx называется доверительной границей случайного отклонения результатов наблюдений, соответствующей доверительной вероятности Р. Для определения доверительной границы (при выполнении перечисленных условий) задаются доверительной вероятностью, например Р=0,95 или Р=0,995 и по формулам
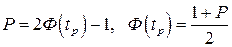
определяют соответствующее значение 2Ф(tp) интегральной функции нормированного нормального распределения. Затем по данным таблицы 1 приложения находят значение коэффициента tp и вычисляют доверительное отклонение tpσx Проведение многократных наблюдений позволяет значительно сократить доверительный интервал. Действительно, если результаты наблюдений Xi (i=l, 2,..., n) распределены нормально, то нормально распределены и величины Xi/n, а значит, и среднее арифметическое, являющееся их суммой. Поэтому имеет место равенство
где tp определяется по заданной доверительной вероятности Р.
Полученный доверительный интервал, построенный с помощью среднего арифметического результатов n независимых повторных наблюдений, в «корень из» n раз короче интервала, вычисленного по результату одного наблюдения, хотя доверительная вероятность для них одинакова. Это говорит о том, что сходимость измерений растет пропорционально корню квадратному из числа наблюдений.
Половина длины нового доверительного интервала
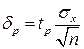
называется доверительной границей погрешности результата измерений, а итог измерений записывается в виде
Теперь рассмотрим случай, когда распределение результатов наблюдений нормально, но их дисперсия неизвестна. В этих условиях пользуются отношением
называемым дробью Стьюдента. Входящие в нее величины вычисляют на основании опытных данных; они представляют собой точечные оценки математического ожидания и среднеквадратического отклонения результатов наблюдений.
Плотность распределения этой дроби, впервые предсказанного Госсетом, писавшим под псевдонимом Стьюдент, выражается следующим уравнением:
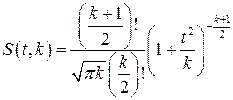
где S(t,k) – плотность распределения Стьюдента. Величина k называется числом степеней свободы и равна n–1. Вероятность того, что дробь Стьюдента в результате выполненных наблюдений примет некоторое значение в интервале (‑tp, +tp), согласно выражению, вычисляется по формуле:
или, поскольку S(t,k) является четной функцией аргумента t,
Подставив вместо дроби Стьюдента t ее выражение через истинное значение результата, точечные оценки математического ожидания и среднеквадратического отклонения результатов наблюдений, получим окончательно
Величины tp, вычисленные по этим формулам, были табулированы Фишером для различных значений доверительной вероятности Р в пределах 0,10 – 0,99 при k=n–1=1,2,…,30. В таблице 5 приведены значения tp для наиболее часто употребляемых доверительных вероятностей Р.
Итог измерений записывается в виде
В тех случаях, когда распределение случайных погрешностей не является нормальным, все же часто пользуются распределением Стьюдента с приближением, степень которого остается неизвестной.
Кроме того, на основании центральной предельной теоремы теории вероятностей можно утверждать, что при достаточно большом числе наблюдений распределение среднего арифметического как суммы случайных величин Xi/n будет сколь угодно близким к нормальному.
Таблица 5– Коэффициент Стьюдента
| k | P | ||||
| 0,8 | 0,9 | 0,95 | 0,98 | 0,99 | |
| 3,08 | 6,31 | 12,71 | 31,8 | 63,7 | |
| 1,89 | 2,92 | 4,30 | 6,96 | 9,92 | |
| 1,64 | 2,35 | 3,18 | 4,54 | 5,84 | |
| 1,53 | 2,13 | 2,77 | 3,75 | 4,60 | |
| 1,48 | 2,02 | 2,57 | 3,36 | 4,03 | |
| 1,44 | 1,94 | 2,45 | 3,14 | 4,71 | |
| 1,42 | 1,90 | 2,36 | 3,00 | 3,50 | |
| 1,40 | 1,86 | 2,31 | 2,90 | 3,36 | |
| 1,38 | 1,83 | 2,26 | 2,82 | 3,25 | |
| 1,37 | 1,81 | 2,23 | 2,76 | 3,17 | |
| l,363 | 1,80 | 2,20 | 2,72 | 3,11 | |
| 1,36 | 1,78 | 2,18 | 2,68 | 3,06 | |
| 1,35 | 1,77 | 2,16 | 2,65 | 3,01 | |
| 1,35 | 1,76 | 2,14 | 2,62 | 2,98 | |
| 1,34 | 1,75 | 2,13 | 2,60 | 2,95 | |
| 1,34 | 1,75 | 2,12 | 2,58 | 2,92 | |
| 1.33 | 1,74 | 2,11 | 2,57 | 2,90 | |
| 1,33 | 1,73 | 2,10 | 2,55 | 2,88 | |
| 1,33 | 1,73 | 2,09 | 2,54 | 2,86 | |
| 1,38 | 1,73 | 2,09 | 2,53 | 2,85 | |
| 1,32 | 1,72 | 2,08 | 2,52 | 2,83 | |
| 1,32 | 1,72 | 2,07 | 2,51 | 2,82 | |
| 1,32 | 1,71 | 2,07 | 2,50 | 2,81 | |
| 1,32 | 1,71 | 2,06 | 2,49 | 2,80 | |
| 1,32 | 1,71 | 2,06 | 2,49 | 2,79 | |
| 1,32 | 1,71 | 2,06 | 2,48 | 2,78 | |
| 1,31 | 1,70 | 2,05 | 2,47 | 2,77 | |
| 1,31 | 1,70 | 2,05 | 2,47 | 2,76 | |
| 1,31 | 1,69 | 2,05 | 2,46 | 2,76 | |
| 1,30 | 1,68 | 2,02 | 2,42 | 2,70 | |
| 1,30 | 1,67 | 2,00 | 2,39 | 2,66 | |
| 1,29 | 1,66 | 1,98 | 2,36 | 2,62 | |
| >120 | 1,28 | 1,65 | 1,96 | 2,33 | 2,58 |
Если эксперимент состоит в многократном измерении одной и той же величины постоянного размера, то результатом измерения является группа из n независимых показаний (измерений), составляющих массив экспериментальных данных. Главной особенностью измерительного эксперимента, проводимого с использованием статистической обработки полученных данных, является получение и использование большого объема апостериорной измерительной информации.
При статистической обработке многократных показаний решаются три основные задачи:
― оценивание области неопределенности исходных экспериментальных данных;
― нахождение более точного усредненного результата измерения;
― оценивание погрешности этого усредненного результата, то есть более узкой области неопределенности.
При практическом выполнении статистической обработки многократных показаний необходимо знание методов определения по экспериментальным данным числовых характеристик распределений случайной величины. Основной смысл усреднения многократных показаний заключается в том, что найденная усредненная оценка координаты их центра имеет меньшую случайную погрешность, чем отдельные показания, по которым она находится. При этом принципиальным является допущение, что показания подчиняются нормальному закону распределения вероятности. Справедливость этого допущения необходимо проверять.
 |
Правдоподобно или нет допущение о том, что полученные показания подчиняются нормальному закону распределения вероятности, можно предварительно оценить по виду гистограммы, построенной на основании полученных экспериментальных данных (рисунок 6).
Рисунок 6 – Гистограмма
Для отображения n полученных показаний СИ в виде гистограммы область численных значений между наименьшим и наибольшим показаниями L = Qmax ‑ Qmin делят на интервалы одинаковой ширины ΔQ и определяют число показаний nk, попавших в каждый из полученных интервалов. Полученные результаты изображают графически, откладывая по оси абсцисс полученные максимальное и минимальное показания с обозначением границ интервалов между ними, а по оси ординат – величину nk/(nΔQ). Построив над каждым из интервалов прямоугольники, основанием которых является ширина интервалов, а высотой – nk/(nΔQ), получим гистограмму, дающую представление о плотности распределения вероятности полученных показаний в данном эксперименте. Относительную частоту попаданий nk/n можно условно приравнять к вероятности попадания в конкретный интервал, а высоту прямоугольника считать равной эмпирической плотности вероятности рk = nk/(nΔQ). Тогда площадь каждого прямоугольника равна вероятности попадания в интервал, а площадь всех прямоугольников будет равна единице, что соответствует условию нормировки (k – число интервалов):
.
Полигон представляет собой ломаную кривую, соединяющую середины верхних оснований столбцов гистограммы. Полученная таким образом кусочнолинейная аппроксимация более наглядно, чем гистограмма, отражает форму искомой кривой распределения
При практической обработке результатов измерений можно последовательно выполнить следующие операции:
1. Записать результаты измерений;
2. Вычислить среднее значение из n измерений:
3. Определить погрешности отдельных измерений Vi = а - аi;
4. Вычислить квадраты погрешностей отдельных измерений Vi2;
5. Если несколько измерений резко отличаются по своим значениям от остальных измерений, то следует проверить не являются ли они промахом. При исключении одного или нескольких измерений п.п.1...4 повторить;
6. Определяется средняя квадратичная погрешность результата серии измерений:
7. Задается значение надежности a;
8. Определяется коэффициент Стьюдента ta(n) для выбранной надежности a и числа проведенных измерений n;
9. Находятся границы доверительного интервала: Dх = ta (n)Sa
10. Если величина погрешности результата измерений (п. 9) окажется сравнимой с величиной d погрешности прибора, то в качестве границы доверительного интервала следует взять величину:
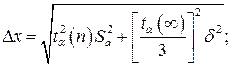
11. Записать окончательный результат: X = a ± Dx;
12. Оценить относительную погрешность результата серии измерений:
13. Результат измерений записывается в виде