Базисные расчетные зависимости для определения интенсивности теплообмена при различных режимах течения в пограничном слое

Рассмотрим наиболее характерные критериальные зависимости конвективного теплообмена.

Задачу поставим следующим образом: на бесконечную тонкую изотермическую пластину с температурой T_w набегает однородный турбулентный поток жидкости (газа) со скоростью U_¥, температурой T_f, давлением p (см. рисунок). При этом, вследствие явления «прилипания» жидкости к стенке, на поверхности пластины, начиная с передней кромки, начинает формироваться пограничный слой, в котором скорость плавно меняется от 0 на стенке до U_¥ во внешнем потоке. Наряду с динамическим (скоростным) пограничным слоем формируется и тепловой, с изменением температуры от T_w до T_f. Режим течения в пограничном слое зависит от местного числа Рейнольдса, построенного по текущей координате: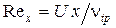. При достижении числом Рейнольдса значения Re_xкр » 5·10⁵ в сечении х_кр происходит переход от ламинарного режима течения в пограничном слое к турбулентному. После этого толщина пограничного слоя турбулентной структуры быстро возрастает, существенно растет и интенсивность теплоотдачи.

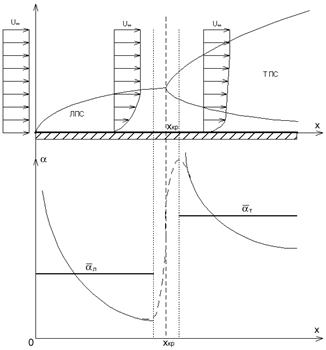Для различных участков течения применяются различные зависимости для теплоотдачи.

1. Локальная теплоотдача на изотермической (T_w=const) пластине при безнапорном обтекании 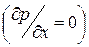и ламинарном пограничном слое.

Теоретическое решение для ламинарного ПС выглядит следующим образом:

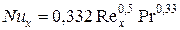; где ;

2. Средний коэффициент теплоотдачи для начального участка длиной l при тех же условиях:

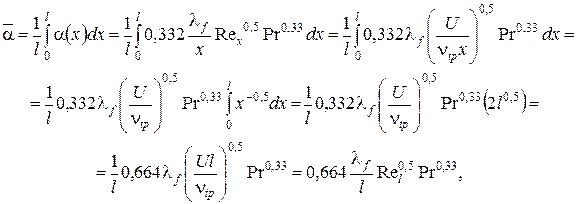
где 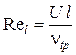, а l – длина начального участка взаимодействия потока и стенки. Таким образом,

.

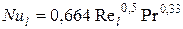3. Эксперимент для средней теплоотдачи пластины и ЛПС:

.

Поскольку определяющая температура здесь T_f, то вводится поправка Михеева на разность термодинамических параметров в основном потоке и на стенке (поправка на “неизотермиченость” потока).

4. Теплообмен вблизи передней критической точки при ЛПС.

При поперечном обтекании на поверхности тела имеется точка или линия, где происходит разделение линий тока, и поток резко меняет направление движения (см. рис.).

Эту точку называют передней критической точкой. Данный тип течения носит градиентный характер, т.е. , и интенсивность теплообмена в нем выше, чем в предыдущем случае.

Набегающий поток может быть плоским или осесимметричным. Рассмотрим плоский поток, набегающий на пластину со скоростью U_¥. Во внешнем потоке после изменения направления течения устанавливается скорость U₀, изменяющаяся вдоль по продольной координате x от сечения к сечению: , где C, m = const. В данном случае m = 1.

Рассмотрим уравнение баланса импульса для внешнего потока (см. уравнение 5 из параграфа 2.1), подставив U₀:

– напор по оси x.

Продольный напор в ламинарном пограничном слое такой же, как во внешнем потоке (см. уравнение 2 § 2.1). Тогда уравнение баланса импульса по x в пограничном слое может быть записано как

.

Для указанной системы уравнений пограничного слоя существует теоретическое решение:

, где .

Градиент давления при таком течении .

Вывод: отрицательный продольный градиент давления приводит к существенному увеличению интенсивности теплоотдачи в ламинарном пограничном слое.

Для осесимметричного набегающего потока:

,

т.е. при осесимметричном растекании потока теплоотдача выше, чем при плоском течении.

5. Локальная теплоотдача ламинарной изотермической (T_w=const) пластины при турбулентном ПС.

Для данного случая имеется теоретическое решение:

.

Здесь координата x отсчитывается от точки перехода от ламинарного режима течения в пограничном слое к турбулентному, y_t – поправка на неизотермичность потока.

 

Кутателадзе и Леонтьев дают следующую зависимость для поправки:

Вывод: в турбулентном пограничном слое теплообмен интенсивнее, чем в ламинарном.

6. Средний коэффициент теплообмена для участка длиной l и ТПС:

.

7. Эксперимент для средней теплоотдачи для участка длиной l и ТПС (с поправкой Михеева):

,

определяющая температура здесь, как и в случае ламинарного ПС, T_f.