Без предварительного преобразования

Методы сопоставления представлены своими четырьмя разновидностями.

Первый метод сопоставления (метод интерполяции) (рис.5.8,а) предполагает использование в наборе элементарных средств измерений многоканальной нерегулируемой меры и устройства сравнения. Многоканальная нерегулируемая мера имеет Nн каналов, обеспечивающих работу по единичной системе счисления с Nн и равномерными ступенями. В набор входит также Nн устройств сравнения при условии реализации одноэтапного алгоритма.

 

 

Рис. 5.8. Структура измерений методом сопоставления:

а – первый метод; б – второй метод;

в – третий метод; г – четвертый метод

 

При условии, что начальные нулевые значения измеряемой и известной величин совпадают, числовое значение определяется по старшему из сработавших устройств сравнения.

Детерминированный алгоритм первого метода сопоставления:

Nxqk < x < (Nk+1)qk.

По этому алгоритму определяют номер старшего из сработавших устройств сравнения:

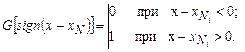(5.9)

При этом по каждому каналу с номером Nх передается единичный сигнал. Так формируется первичный единичный многоканальный код , который и представляет числовое значение измеряемой величины. В дальнейшем этот код преобразуется обычно в цифровой код. Уравнение метода:

.

При несовпадении начальных нулевых отметок измеряемой и известной величин появляется погрешность квантования с обеих сторон интервалов.

Метод используется при измерении напряжения, перемещения и времени.

Одним из вариантов первого метода сопоставления является метод одноэтапного нониуса, основанный на использовании двух многоканальных нерегулируемых мер с различными шагами квантования q1 и q2. Метод используется при х<q1.

При кратности повышения чувствительности n должно соблюдаться соотношение

q2=q1(1-1/n). (5.10)

Графически метод нониуса представлен на рис.5.9. В момент измерения нулевые отметки двух многоканальных нерегулируемых мер оказываются сдвинутыми на величину х. Отсчет делается по номеру ближайшей из «совпавших» отметок. Алгоритм метода измерения:

Nxq1-(x+Nxq2)<q1/n. (5.11)

 

Рис. 5.9. Графическое представление метода нониуса

 

Считая, что q1/n пренебрежимо мало, с учетом (5.10) получаем уравнение метода однократного нониуса:

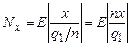. (5.12)

Получается, что шаг квантования как бы уменьшается в n раз. Метод нониуса чаще всего применяется для измерения перемещений и иногда малых интервалов времени.

При относительных измерениях, т.е. при определении отношения

,

q1 – опорное значение шага квантования может оставаться неизвестным, так как важно, чтобы было известным отношение ql1/q2=1-1/n. Это оказывается очень удобным при измерении фазы.

Часто применяемыми вариантами метода нониуса являются метод растра и метод муара.

Метод растра предполагает использование двух многоканальных мер в виде прозрачных линеек (рис. 5.10,а) с близкими размерами шага квантования .

При параллельном наложении меток одной линейки на метки другой образуются тени – участки с максимально сближенными метками. В процессе измерения расстояние между нулевыми метками должно увеличиваться плавно от 0 до lх. Перемещение одной из линеек вызовет перемещение теней на расстояние в n раз больше, чем lx. Результат измерения равен числу меток в ряду , пересеченных тенью:

,

что совпадает с уравнением измерения методом нониуса.

 

 

Рис. 5.10. Схематическое представление методов растра (а) и муара (б)

Метод муара так же, как и метод растра, предполагает использование двух многозначных мер – прозрачных линеек с штриховыми метками (рис. 5.10,б) в виде параллельных равноотстоящих линий.

В отличие от растровых многоканальных мер штриховые метки муаровых линеек имеют одинаковый шаг квантования и при параллельном совмещении линеек располагаются под небольшим углом друг от друга. В процессе измерения, когда одна из линеек плавно перемещается в продольном направлении от 0 до lх, теневые полосы движутся в поперечном направлении, и перемещение в 1/sina больше lх. Результат измерения получают путем счета количества меток, пересеченных тенью, с помощью третьей меры с шагом квантования ql , расположенной перпендикулярно первым двум мерам. Тогда

Nx = lx / sina ql .

Второй метод сопоставления отличается от первого тем, что используемая в нем мера является одноканальной, а для получения количественного результата используется многоканальный нерегулируемый масштабный преобразователь (см.рис.5.8,б). Такой набор позволяет обеспечить минимальное время измерения. Если нерегулируемый масштабный преобразователь является равноступенчатым делителем с коэффициентом передачи

,

где Nн - шаг деления, то алгоритм метода N/Nнx < x0 < (N+1) / Nнx , откуда .

Уравнение измерения:

. (5.13)

Третий метод сопоставления отличается от первого наличием в наборе элементарных средств измерений предвключенного одноканального нерегулируемого масштабного преобразователя (см.рис.5.8,в). Алгоритм метода:

(5.14)

Уравнение измерения:

. (5.15)

Четвертый метод сопоставления предполагает наличие в наборе двух многоканальных неуправляемых средств измерений - меры и масштабного преобразователя (см.рис.5.8,г). Другое название метода - метод коинциденции (одновременного попадания). Чаще всего метод применяют при измерении шага lx штриховых меток и периода Tx или частоты импульсов.

Если нужно измерить lx, смещаются метки как меры, так и масштабного преобразователя до совпадения нулевых отметок и затем определяются номера N’x и N’’x пары "совпадающих" меток рядов меры и масштабного преобразователя соответственно.

Алгоритм метода:

. (5.16)

Уравнение измерения:

, (5.17)

где ql - шаг квантования меры.

В связи с тем, что в измерении участвует два многозначных средства измерений, метод измерений является избыточным, благодаря чему шаг квантования меры qi уменьшается в N'’x раз.

При измерении периода Tx импульсного сигнала

,

где T0 - период меры.

Методы измерений, основанные на уравновешивании измеряемой величины известной величиной по многоэтапному алгоритму, можно объединить в группу методов уравновешивания. Для таких методов характерно использование регулируемых мер и масштабных преобразователей. Причем выходная величина меры или масштабного преобразователя изменяется до тех пор, пока устройство сравнения не зафиксирует равенство измеряемой величины х и квантованной ступенчато изменяющейся величины xN, или равенство между величиной на выходе масштабного преобразователя хКМП и постоянным значением х0, воспроизводимым мерой. Процесс изменения xN или хКМП проходит последовательно во времени, поэтому методы уравновешивания по быстродействию уступают методам сопоставления. Отличительной чертой методов уравновешивания является также и то, что числовое значение измеряемой величины определяется по входному коду меры или коэффициенту преобразования КМП масштабного преобразователя в момент срабатывания устройства сравнения при достижении равенства х и х0.

Рассмотрим сначала подгруппу методов уравновешивания, в которую входят методы с набором, состоящим из двух видов элементарных средств измерений: меры и устройства сравнения.

Первый метод уравновешивания, или нулевой метод измерения (рис.5.11,а), предполагает использование одноканальной регулируемой меры, управляемой оператором или автоматически по знаку разности х-хN на выходе устройства сравнения. Причем выходная величина меры хN изменяется до момента уравнивания со значением х.

 

аi

 

 

Рис.5.11. Структуры измерений методами уравновешивания:

а – первый; б – с удвоением разностей; в – ускоренного уравновешивания;

г – многократного нониуса

 

Нулевой метод измерения является наиболее распространенным благодаря простоте и минимальным аппаратурным затратам.

Отработка выходной величины меры может проходить как по детерминированным алгоритмам с использованием различных систем счисления (единичной, двоичной, двоично-десятичной и др.), так и по стохастическому, когда величина изменяется случайно, но имеет заданное распределение.

Наиболее распространены детерминированные алгоритмы "исчерпывания" и поразрядного уравновешивания.

Алгоритм "исчерпывания":

(5.18)

;

В данном случае размер qk реализуется последовательными ступенями изменяющейся во времени выходной величины меры. Каждая ступень инициируется импульсом. В момент равенства х и выходной величины меры число импульсов равно Nx, выражаемому первично в одноканальном последовательном коде, который в цифровой форме с помощью счетчика импульсов может быть представлен двоичной (или иной) кодовой комбинацией:

. (5.19)

Алгоритм поразрядного уравновешивания:

(5.20)

где m - количество разрядов двоичного кода, - значение выходной величины меры, соответствующее i -му разряду двоичного кода.

Результат измерения в двоичном коде:

; (5.21)

при <0 am=0 ;

при >0 am=1 ;

при x-(am +am-i )<0; am-i=0 ;

при x-(am +am-i )<0; am-i=1.

Результат измерения в виде числового значения Nx представляется первично в двоичном или ином цифровом коде.

Аппаратурная реализация метода несколько сложнее, чем при поразрядном уравновешивании, но быстродействие увеличивается в раз.

Статистический алгоритм первого метода уравновешивания рассмотрим на примере алгоритма отработки среднего значения случайного процесса х(t). Выходная величина одноканальной регулируемой меры в данном случае принимает случайные значения, подчиняющиеся равномерному закону распределения вероятностей, что может быть реализовано, например, при управлении мерой в пределах чисел от 0 до Nx от генератора случайных чисел. Максимальное значение xm(t) должно быть меньше номинального значения выходной величины меры xNн.

Описание алгоритма:

(5.22)

Отработка производится до тех пор, пока частость срабатывания n0/n устройства сравнения при (x – xNi) >0 не будет равна отношению xср/xNн, тогда

.

Второй метод уравновешивания, называемый методом с удвоением разностей, характеризуется использованием одноканальной нерегулируемой меры и одного устройства сравнения (см.рис.5.11,б). Отличительной особенностью метода является создание и удвоение разностей с последующим сравнением выходной величины меры с создаваемыми разностями.

Третий метод уравновешивания - метод ускоренного уравновешивания - основан на использовании многоканальной регулируемой меры и N устройств сравнения (см.рис.5.11, в).

Уравнение метода:

x = Nxqk .

Ускорение процесса уравновешивания достигается за счет многоканальности меры и увеличения числа используемых устройств сравнения, чем обеспечивается пространственное и временное разделения. Крайним случаем является развертка выходной величины меры во всех квантах одновременно.

Метод многократного нониуса (четвертый метод уравновешивания) реализуется с помощью трех и более многоканальных нерегулируемых мер и ряда устройств сравнения (см.рис.5.11, г).

Уравнение метода:

x-Nq-N1(q1-q2)-N2(q1-q3)£q1-q3.

Такой метод применяется, если размер ступени мер не отвечает требованиям чувствительности и точности и требуется повысить быстродействие.

Подгруппу методов измерений с использованием универсальных средств измерений трех видов - меры, устройства сравнения и масштабного преобразователя - составляют девять методов измерений. На схеме рис. 5.7 эти методы обозначены как 2-3-й методы уравновешивания, 2-5-й методы ускоренного уравновешивания, 1-2-й стробоскопические методы. Числовые обозначения методов даны условно с целью идентификации каждого из них. По этой схеме можно определить набор элементарных средств измерений для соответствующих методов измерения.

Уравнения методов рассматриваемой подгруппы:

второго метода уравновешивания

KМПрx = x0 ,(5.23)

где КМПр - коэффициент преобразования одноканального регулируемого масштабного преобразователя;

третьего метода уравновешивания -

xКМП=x0КМПр=Nxqk ; (5.24)

второго-пятого методов ускоренного уравновешивания соответственно -

xNx/Nн=x0; xNx/Nн=x0KМр; xKМПр=Nxqk; xKМП=Nxqkр , (5.25)

первого и второго стробоскопических методов соответственно -

TxKМПр=T0; Tx=T0KМПр . (5.26)

Последние два метода получили такое название в связи с тем, что в устройстве сравнения используется стробоскопический эффект. В момент уравновешивания срабатывают все устройства сравнения. Измерению подлежат величины частотно-временной группы - частота и период. Уравновешивается период (или частота) изменением известного периода Т0 либо коэффициента масштабного преобразователя. С помощью стробоэффекта определяется знак разности, равенства или кратности сравниваемых величин.

Одним из наиболее часто применяемых методов является дифференциальный метод измерений (рис. 5.12).

Во многих случаях при реализации дифференциального метода находят применение комбинированные прямые измерения без предварительных преобразований. Процедура таких измерений состоит из двух этапов: сначала измерения производятся одним из рассмотренных методом сопоставления или уравновешивания, а затем разность измеряемой величины и выходного сигнала меры измеряется другим (или таким же, как на первом этапе) методом. На втором этапе измерений нередко используются комплексные средства измерений.

 

 

Рис. 5.12. Дифференциальный метод измерения:

а - с применением на первом этапе нерегулируемой меры;

б - с применением на первом этапе регулируемой меры

 

Возможны два варианта реализации: первый с применением на первом этапе нерегулируемой меры (см.рис.5.12,а), второй с применением регулируемой меры (см.рис.5.12,б). В обоих вариантах устройство сравнения используется в качестве вычитателя В с выходной величиной в виде разности Dр измеряемой и известной величин.

В первом варианте с помощью меры воспроизводится постоянное значение х0 и на выходе вычитателя получается разность Dp=x-x0, которая на втором этапе измеряется комплексным средством измерения. Результат измерения получается суммированием результатов обоих этапов. Такой вариант дифференциального метода применяют при близких значениях х и х0, когда точность измерения зависит только от погрешности меры.

Во втором варианте дифференциального метода на первом этапе с помощью регулируемой меры создается величина x1=Nxqk, однородная с х и близкая к ней по значению. Получаемая на выходе вычитателя В разность Dp=x-Nxqk измеряется на втором этапе с помощью комплексного средства измерений, затем результаты суммируются.

Отсчет по комплексному СИ

nx=Dp/qпр ,

где qпр - шаг квантования комплексного СИ.

Тогда результат измерений

XN = Nxqk + nxqпр . (5.27)

Очевидно, суммарная погрешность измерений при реализации метода будет зависеть как от точности меры (определяемой первым слагаемым), так и от точности комплексного средства измерений (второе слагаемое). Если принять Nxqk>>nxqпр, то точность измерения будет зависеть главным образом от точности шага квантования выходной величины меры.