Диадические игры

Игры, в которых каждому участнику предоставляется только две чистые стратегии, называются диадическими. Участник , участник , участник .

В диадических играх смешанная стратегия участника 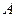описывается вероятностью , так как . Поэтому решить диадическую игру – значит найти оптимальные .

Продемонстрируем метод решения диадических игр на примере из [2]. Имеются предприятия: 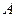, 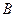и , осуществляющие сброс воды в один водоем. Каждый из них имеет две чистые стратегии:

– используют очистные сооружения;

– не используют очистные сооружения.

Водоем такой, что если два или более предприятий сбрасывают неочищенную воду, то вода загрязняется выше нормы, и все предприятия платят штраф (-3). Использование очистных средств обходится предприятию в (-1).

Для каждого из участников должны быть заданы матрицы полезности:.

Удобно представить эти матрицы графически на кубе (рис. 2.10).

Углы куба – возможные исходы (в скобках указаны расходы трех предприятий при соответствующем исходе ).

Зафиксируем стратегии участников 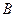и

.

 

Приемлемая смешанная стратегия – это лучшая стратегия для участника 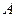при фиксированных .

– зависимость приемлемой стратегии от ,

– зависимость приемлемой стратегии от ,

– зависимость приемлемой стратегии от .

 

Рис. 2.10. Графическое представление матриц полезностей для участников

 

Найдем оптимальные стратегии для всех участников на пересечении этих функций. Построим эти функции для нашего примера. Так как у нас в примере игра симметричная, то достаточно построить одну зависимость .

При первой чистой стратегии выигрыш будет:

,

а при второй чистой стратегии :

.

Чтобы первая стратегия была приемлемой, она должна быть лучше второй, поэтому первый выигрыш должен быть не хуже второго.

Сгруппируем слагаемые:

С учетом, что , получим условие когда – приемлемая:

 

Введем обозначения:

 

С учетом обозначений получим неравенство:

.

В нашем примере:

Получаем неравенство, определяющее соотношения между и , когда будет приемлемой стратегией:

.

Отсюда получаем области: , показанные на рис. 2.11.

 

 

 

 

Рис. 2.11. Множество приемлемых стратегий для участника А при

 

На рис. 2.12 приведена зависимость :

 

Рис. 2.12. Множество приемлемых стратегий для участника А

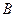Аналогично будут выглядеть зависимости и для участников и .

Результат пересечения и приведен на рис. 2.13:

 

 

Рис. 2.13. Пересечение множеств приемлемых стратегий

 

Интерпретация решения. Точка (1) соответствует ситуации безнадежности, когда все фирмы не строят очистные сооружения.

Точки (2), (3), (4) – наличие "нахала" – две фирмы строят, а одна – нет.

Точки (5), (6), (7) соответствуют тому, что один строит очистительные сооружения, а два других уменьшают свои сбросы (сознательное природопользование):

.

Точки (8), (9) находятся на диагонали куба, и их координаты получают из условия:

.

Из-за симметрии , и получается уравнение:

Точка 8={0,211; 0,211; 0,211} – справедливое решение, а точка 9 {0,789; 0,789; 0,789} – ближе к безнадежной точке (1).