Аналитический расчет термических напряжений при конвективном нагреве цилиндрических тел
В разделе 4.1 приведены аналитические решения для расчета относительных термических напряжений в любой точке неограниченной пластины при ее конвективном нагреве в печи с постоянной температурой греющей среды  - см. уравнения (4.1)…(4.55).
- см. уравнения (4.1)…(4.55).
Из анализа этих уравнений следует, что динамика изменения напряжений во времени аналогична изменению температурной разности, т.е. резко возрастают, достигая максимального значения при числах Фурье Fomax=0,05…0,50, а затем постепенно падают, т.е. носят колоколообразный характер.
На практике иногда важнее знать не всю динамику изменения напряжений во времени, а только их максимально возможные характерные величины, например, на поверхности и в центре тела. Целью данного раздела является аналитическое определение указанных величин для цилиндрических тел.
В монографии Н.Ю. Тайца [7] показано, что для цилиндрических тел следует различать термические напряжения:
радиальные на поверхности
 , (4.56)
, (4.56)
тангенциальные на оси
 , (4.57)
, (4.57)
и осевые
 . (4.58)
. (4.58)
Из одинаковости выражения (4.58) с формулой (4.2) вытекает, что формулы для расчета осевых напряжений в цилиндре совпадают с формулами (4.2)...(4.4) для пластины и можно ограничиться анализом этих уравнений. Поэтому задачу определения термических напряжений в цилиндре будем решать в предположении такой же их зависимости от температур на поверхности, в центре и среднемассовой как для плоских тел.
Для цилиндрических тел будут справедливы уравнения (4.2)...(4.8), (4.10), (4.11) для пластины с заменой координатной функции  , входящей в уравнение (4.5)
, входящей в уравнение (4.5)  , тепловых амплитуд
, тепловых амплитуд  для уравнения (4.6),
для уравнения (4.6), 
 — для (4.7) и
— для (4.7) и  — для (4.8). Теперь корни
— для (4.8). Теперь корни  вместо (4.9) определяются из характеристического уравнения:
вместо (4.9) определяются из характеристического уравнения:
 , (4.59)
, (4.59)
где  и
и  — функция Бесселя первого рода нулевого и первого порядка.
— функция Бесселя первого рода нулевого и первого порядка.
Дифференцируя уравнения (4.3), (4.4) и (4.10) по времени, приравнивая производную нулю и используя два члена суммы ряда, получим формулы для расчёта максимальных времен Фурье:
для максимального термического напряжения на поверхности
 , (4.60)
, (4.60)
перепада температур
 (4.61)
(4.61)
и термонапряжения в центре
 , (4.62)
, (4.62)
где  ;
;  ;
;  ;
;  ;
;  .
.
Здесь и далее под 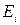 понимается амплитуда
понимается амплитуда  .
.
Подставляя Fоmах из (4.61) в уравнение (4.55), получим максимальный перепад температур с учётом двух членов ряда:
 (4.63)
(4.63)
При выводе (4.63) было учтено, что согласно уравнению (4.61)  .
.
По аналогии подставляя  в уравнение (4.3), получим максимальное термическое напряжение на поверхности
в уравнение (4.3), получим максимальное термическое напряжение на поверхности
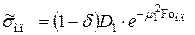 (4.64)
(4.64)
и после подстановки (4.62) в (4.4) — максимальное напряжение в центре цилиндра
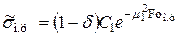 . (4.65)
. (4.65)