Метод наименьших квадратов (МНК)

 

Рассмотрим задачу “наилучшей” аппроксимации набора наблюдений X_t, Y_t, t = 1, 2, …, n линейной функцией f(X) = a + bX в смысле минимизации функционала

. (7)

Запишем необходимые условия экстремума:

;

;

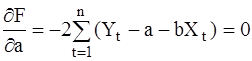(8)

 

Раскроем скобки и получим стандартную форму нормальных уравнений (для краткости опустим индексы суммирования у знака суммы):

(9)

– решения системы (9) можно легко найти:

, (10)

 

. (11)

 

Замечание 1. Из первого уравнения системы следует

, (12)

 

т.е. уравнение прямой линии , полученное в результате минимизации функционала (7), проходит через точку 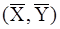. Здесь через обозначены средние значения :

;

.

Замечание 2. Мы предполагаем здесь, что среди X_t, t = 1, 2, …, n не все числа одинаковые, т.е. Var(X)≠0 и уравнение (10) имеет смысл.