Закон равной вероятности.
Если непрерывная случайная величина при испытаниях принимает все значения интервала х с одинаковой плотностью вероятности, то распределение вероятности графически будет выражаться в виде прямоугольника, с основанием аb и высотой f(х) (рис.а).
f(x) F(x)
M(x) 1
0,5
f (x)
M(x)
X X
Рис. а) Рис. б)
Такой закон распределения н.с.в. называется законом равной вероятности, а само распределение - равномерным. При интервале изменений случайной величины Х от а до b:
Р( а < X < b ) = 
f(x)d(x) = 1,
т.е., вероятность того, что случайная величина x при испытаниях будет принимать значения в интервале от a до b, равна площади под дифференциальной кривой распределения. В соответствии с рис. a), эта площадь представляет собой прямоугольник с основанием ab и высотой f(x). Следовательно, (b – a) f(x) = 1.
Отсюда, уравнение дифференциальной функции распределения или плотности вероятности будет иметь следующий вид:
1/(b – a) при a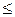 
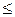x b;
f(x) =
0 при x > b, x < a.
Математическое ожидание, дисперсия и с.к.о. соответственно равны: М(х) = (b + а)/2; D(x) = (b – a )2/12; 
(x) = (b – a)/2
.
Применение закона. Закон наблюдается в тех случаях, когда на исследуемую величину оказывает влияние резко доминирующий фактор, равномерно изменяющийся во времени ( например, равномерный износ инструмента).
3.6. Закон распределения эксцентриситета (Релея).
Закон распределения эксцентриситета имеет место при отклонениях эксцентриситета осей или биении поверхностей деталей, которые являются н.с.в. Этот закон однопараметрический, и дифференциальная функция его распределения имеет вид:
f(R) =(R/2)e-R
/2,
где R – переменная величина эксцентриситета или биения,
причем R =
, а x и y - координаты точки конца R (рис.а); - среднее квадратическое отклонение значений координат х и y, имеющих одинаковое распределение:= х = y.
Интегральный закон распределения эксентриситета имеет выражение: F(R) = 1/2
Re-R/2dR.
Графическое изображение дифференциального закона распределения дано на рис. б).
y
f (R)
y
y
 | |||
 | |||
Рис.2 R
 | |||||
 |  | ||||
Рис. 1 x R=
Особенностью данного распределения является то, что в основе его лежит нормальное распределение, так как координаты х и y точки конца R распределены нормально, а само распределение не является нормальным. Связь междуR, M(R) и представлена следующими зависимостями:
M(R) = 
; R = 
;
Закон Релея можно ожидать в следующих случаях:
а) при несоосности двух номинально соосных цилиндрических поверхностей (эксцентриситет, биение);
б) при непараллельности двух образующих цилиндрических
поверхностей;
в) при непараллельности двух плоскостей;
г) при непараллельности двух плоскостей или осей к плоскости;
д) при разностенности.