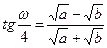Общая теория картографических проекций

Картографическая проекция – математически выраженный способ отображения Земли или другого небесного тела принимаемого за шар или эллипсоид на плоскости. Общие уравнения карт. пр. имеют вид:

x=f₁ (j, l) (1)

y=f₂ (j, l)

j, l – геогр. координаты некоторой точки на картографируемой пов-ти, x и y – прямоугольные координаты изображения этой точки на пл-ти в проекции, определяемой функциями f₁ и f₂, при условии, что эти ф-и однозначны и непрерывны.

Св-ва пр. и будут зависеть от этих ф-ций. Поскольку этих функций множ-во, то получаемые пр-ции тоже м.б. разнообразными.

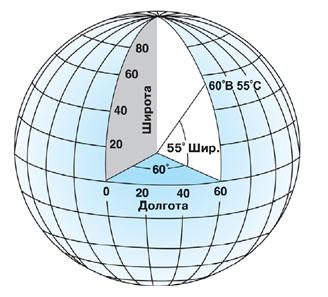
Каждой пр-ции соответствует определённая картографическая сетка мер. и пар., к-рая составляет матем. осн. создаваемых карт.

Положение мер. и пар. на картогр пов-ти определяется географическими координатами: широтой j и долготой l. Широта – это угол мж плоскостью экватора и нормалью в данной точке. Долгота – угол мж плоскостью начального мерид. и плоскостью, проходящей через данную точку.

Геодезические широта и долгота отличаются от соответствующих астрономических координат, связанных с отвесной линией, так как отвесная линия не совпадает с нормалью к эллипсоиду.

Каждая карта имеет главный м-б, который показывает общую степень уменьшения всей картографируемой территории при изображении на плоскости. Гл. м-б подписывается на карте, но сохраняется только в отдельных точках или на некоторых линиях карты. Поскольку главный масштаб на карте является величиной переменной, вводится понятие частных м-бов длин и площадей в данной точке.

Частным м-бом длин называется отношение длины беск. малого отрезка на карте ds` к длине соответствующего беск. малого отрезка на пов-ти эллипсоида или шара ds

m= ds`/ ds (2)

Искажением длин (v_m) называется разность мж частным масштабом длин и единицей, выраженная в процентах, например

m=1.20, v_m = (m-1) * 100%=+20%

n=0.78 v_n = (n-1) * 100%=-22%

Частным масштабом площадей называется отношение бесконечно малой площади на карте (в проекции) к соответствующей б.м. площади пов-ти эл-да или шара

p = dF`/dF. (2*)

Как правило, dF`≠dF, но сущ-ют р/вел картографические пр-ции, в каждой точке к-рых dF`=dF. Ч.м. зависит от геогр. положения эл-та площади, т.е. от широты и долготы.

Искажением площадей (v_p) наз. разность между м-бом площадей и единицей, выраженная в процентах

v_p=(p-1) * 100%

Искажения углов (∆u) характеризуются разностью между величиной угла в проекции (u`) и величиной соответствующего угла на картографируемой пов-ти (u). Как правило, эти углы не равны, но существуют р/уг пр-ции, в каждой точке которых u`= u.

∆u = u`– u.

Величины искажений являются одним из основных критериев оценки достоинства карт. произведений.

 

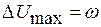
4.3.1. Масштаб длин, масштабы по меридианам и параллелям

 

Из (2) масштаб длин:

m= ds`/ ds

но

- б.м. отрезок на карте

- б.м. отрезок на пов-ти эллипсоида (из сферического треугольника)

В этом треугольнике б.м. дуга меридиана

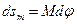, где М – радиус кривизны меридиана.

, где r – радиус кривизны параллели, r=Ncosφ, N – радиус кривизны первого вертикала. Подставляя в (2) формулы (*), получим

 

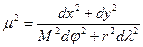
Введём известные коэффициенты Гаусса:

.

 

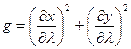
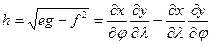Тогда

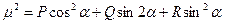(3), где

; ; .

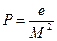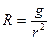При

α = 0° µ² = m² =P,

масштаб по меридианам

;

при

α = 90° µ² = n² =R,

масштаб по параллелям

.

 

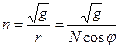4.3.2. Изображение линейного элемента (азимута) в проекции

 

Азимут произвольного направления α в проекции обозначим через β. Для определения β построим на плоскости изображение элементарной сфероидической трапеции.

Найдём угол ψ, который образует элементарный отрезок ds с положительным направлением оси Х

Пользуясь этой формулой, можем найти также углы γ_m и γ_n, к-рые образуют с положительным направлением оси Х меридианы и параллели (или касательные к ним). Принимая j=const для параллели и l=const для меридиана, найдём

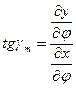
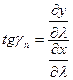
Найдём азимут элементарного отрезка ds: 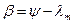, тогда путём преобразований получим

На основании рисунка м. получить угол i между изображениями меридианов и параллелей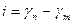

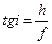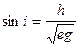; (4)

Вместо угла i в мат. карт. обычно пользуются углом ε, к-рый показывает уклонение угла между меридианами и параллелями от 90^о, эта величина характеризует неортогональность картографической сетки

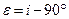
И тогда

Для того, чтобы сетка была ортогональна, показатель неортоганальности ε д.б. равен нулю, т.е. ε = 0, когда f = 0, т.е. условие ортогональности выполняется.

 

4.3.3. Эллипс искажений. Максимальный и минимальный масштабы длин.

Возьмём на картографируемой пов-ти окр-ть б.м. радиуса и исследуем, как эта окружность будет изображаться в пр-ции. Из т. А', к-рая явл. изобр-ем заданной на картографируемой пов-ти т. А, проведём напр-я, совп. с напр. меридиана, принятым за ось Х, углы β₁, β₂ и т.д. На этих направлениях отложим отрезки, численно равные значениям масштаба длин μ₁, μ₂ и т.д.

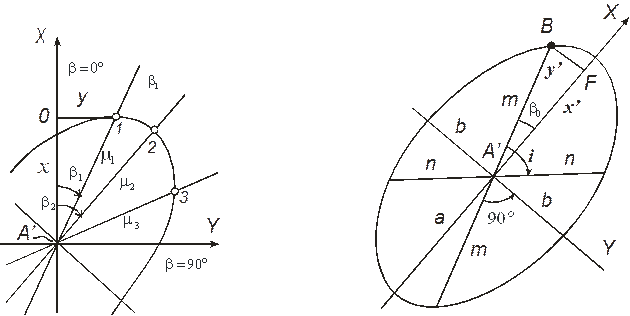Соединив конечные точки этих отрезков, мы получим кривую, которая хар-ет изм-е м-ба длин в зависимости от азимута.

Приняв т. А' за начало прямоуг. кд и за полюс плоских полярных координат (β и μ), м. написать

, .

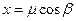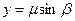Тогда

, .

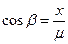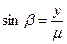Подставим эти значения в (3), и установим, что исследуемая кривая является эллипсом. Следовательно, б.м. эллипс в каждой точке на карте, являющейся отображением б.м. круга на пов-ти эл-да или шара, наз. эллипсом искажений.

Примем, что меридианы и параллели проходят ч/з оси X' и Y', совпадающие с главными направлениями

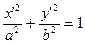
Известно, что

;

.

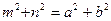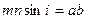Решим эти уравнения совместно и получим искомые экстремальные масштабы:

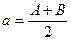, , где (5)

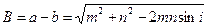
Значение i известно из (4).

 

4.3.4. Масштаб площадей и максимальное искажение углов

 

Из (2*) известно, что p=dF'/dF.

Путём преобразований получим p=ab=mncosε

Максимальное искажение углов ω:

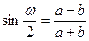
или