ПРЯМАЯ ЛИНИЯ
Проекции прямой линии на плоскость есть прямая. Отсюда следует, что для построения проекций прямой достаточно построить проекции двух точек, ей принадлежащих, и соединить их одноименные проекции прямыми линиями (рис. 1.7).
В зависимости от расположения прямых в пространстве относительно плоскостей проекций различают три вида прямых: прямые общего положения, прямые уровня и проецирующие прямые. На рис 1.7 изображены проекции прямой n (прямой общего положения), не параллельной и не перпендикулярной к плоскостям проекций. Проекции отрезка прямой n меньше его истинной длины: A1B1<AB; A2B2<AB. Различают три типа прямых уровня: горизонтальную, фронтальную и профильную прямые.
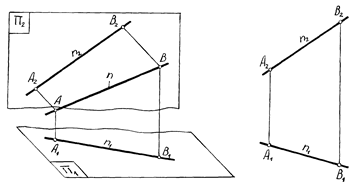
Рис. 1.7
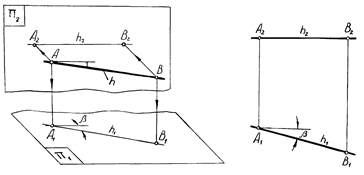
Рис. 1.8

Рис. 1.9
К прямым уровня относятся прямые, параллельные какой либо из плоскостей проекций. Прямая, параллельная горизонтальной плоскости проекций, называется горизонтальной прямой или горизонталью – h (рис. 1.8). Все точки этой прямой имеют одну и ту же высоту, следовательно, ее фронтальная проекция h2 параллельна оси x (перпендикулярна к вертикальной линии связи). Угол b, образованный горизонтальной проекцией h1 и осью x является углом наклона прямой к фронтальной плоскости проекций. Горизонтальная проекция отрезка AB, принадлежащего этой прямой, равна его истинной длине: A1B1=AB.
Прямая, параллельная фронтальной плоскости проекций (рис. 1.9), называется фронтальной прямой или фронталью – f. Все точки прямой имеют одну и ту же глубину, следовательно, ее горизонтальная проекция на комплексном чертеже параллельна оси x (перпендикулярна к линии проекционной связи). Угол, образованный фронтальной проекцией и осью x, определяют истинную величину угла наклона прямой к горизонтальной плоскости проекций. Фронтальная проекция какого-либо отрезка, принадлежащего прямой, равна его истинной длине.
Прямые, перпендикулярные к одной из плоскостей проекций, называют проецирующими. На рис. 1.10 изображена горизонтально проецирующая прямая t, перпендикулярная к горизонтальной плоскости проекций. Горизонтальная проекция прямой t вырождается в точку, а фронтальная совпадает с вертикальной линией связи. Прямая m, перпендикулярная к фронтальной плоскости проекций, носит название фронтально проецирующей прямой. Фронтальная проекция прямой m вырождается в точку, горизонтальная – совпадает с линией вертикальной связи.
Из сказанного следует, что одноименные проекции точек, принадлежащих этим прямым, совпадут с проекциями самих прямых: t1ºA1ºB1, m2ºC2ºD2. Такие точки принято называть конкурирующими. Точки A и B, принадлежащие горизонтально проецирующей прямой t, называют горизонтально конкурирующими, точки C и D, принадлежащие фронтально проецирующей прямой m, - фронтально конкурирующими.
В качестве примера определим длину отрезка прямой общего положения. Это можно осуществить с помощью построения прямоугольного треугольника, одним из катетов которого является проекция отрезка AB на плоскость P1 (рис. 1.11). Гипотенуза A1B* прямоугольного треугольника представляет собой истинную длину отрезка, а угол a определяет угол наклона прямой к плоскости проекций P1. Длину отрезка и угол наклона прямой к плоскости проекций P2 можно определить, построив прямоугольный треугольник на фронтальной проекции отрезка.
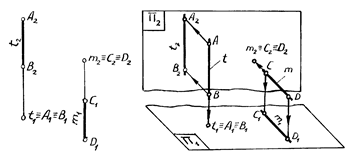
Рис. 1.10

Рис. 1.11