Геометрические вероятности

Это понятие касается следующего класса задач. Представим себе, что на плоскости расположены две области 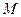и , причем область целиком распложена в области 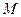. Их площади, соответственно, равны и . В область 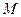наудачу бросают точку. Какова вероятность того, что точка попадёт также и в область ?

Если предположить, что точка может попасть в любую часть области 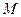, а вероятность попадания в область пропорциональна лишь её площади и не зависит ни от расположения , ни от её формы, то искомая вероятность:

.

Это и есть так называемое «правило нахождения геометрической вероятности» [7].

Аналогично могут быть определены вероятности попадания точки:

1) в объёмную область величиной , содержащуюся в объёмной области величиной , если точка брошена наугад в объём :

;

2) на отрезок 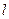величиной , расположенный на отрезке величиной , если точка брошена наугад на отрезок :

.

 

 

Пример. Круглый диск радиуса разбит на два сектора. Длина дуги одного из них (заштрихованного) равна радиусу (рис. 2.2). По быстро вращающемуся диску произведён выстрел. Цель поражена. Найти вероятность того, что попали в заштрихованную часть.

Рис. 2.2. Иллюстрация к задаче о попадании в сектор диска

 

Решение. Идеология решения задачи проста. Пусть событие 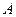есть событие, состоящее в том, что попали именно в заштрихованную часть. Тогда искомая вероятность равна , где - площадь заштрихованной части, - площадь круга ().

Проблема лишь в том, как найти площадь заштрихованной части. Но относится к также, как длина дуги заштрихованной части () относится к длине круга (): , что и требовалось найти.

___________________________________________

Пример. Задача Бюффона (или задача об игле) [7]. Пусть на плоскость, разлинованную параллельными линиями с расстоянием , наудачу брошен отрезок (игла) длиной . Какова вероятность пересечения линии иглой?

Событие 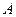состоит в пересечении линии на плоскости. Игла пересекает только одну линию в силу ограничения , или не пересекает ни одной. Пусть - расстояние от центра иглы до ближайшей линии, а - угол наклона иглы к линиям. Тогда множество всех равновозможных событий , а множество всех благоприятствующих исходов для события и оба эти множества изображены ниже на рисунке. Вероятность события 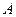вычисляется как геометрическая:

, , .

Рис 2.3. Иллюстрация к задаче Бюфона