Вычисление систематических погрешностей измерений.

 

Прямые измерения.

а) При вероятности Р = 1 находят предельные значения погрешности измерения Δ_п путём арифметического суммирования предельных значений составляющихΔ_i,п:

Δ_п = ± . (20)

Составляющими могут быть:

– основная погрешность Δ_о,п;

– дополнительные погрешности Δ_д,п;

– погрешность отсчитывания Δ_отс,п;

– погрешность взаимодействия Δ_вз,п.

При таком способе суммирования плохо то, что получается сильное завышение погрешности, ибо очень мало вероятно, чтобы все составляющие оказались на своих пределах и были при этом одного и того же знака (плюс или минус). Зато этот способ даёт полную гарантию.

б) При вероятности Р < 1, например, при Р = 0,95, находят граничные значения погрешности измерения Δ_гр путём статистического суммирования предельных значений составляющихΔ_i,п:

 

Δ_гр = ± К. (21)

 

Значение К зависит от законов распределения случайных величин Δ_i и от задаваемого значения вероятности Р. Если законы распределения неизвестны, рекомендуется принять, что для всех составляющих это закон равномерной плотности. При этом из теории вероятностей следует, что значения К при разных значениях Р соответствуют приведённым в таблице 1:

 

Таблица 1.

Р	0,9	0,95	0,99
К	0,95	1,1	1,4

 

Значение Δ_гр может быть существенно меньше по сравнению с Δ_п, хотя Р близко к единице. Максимальное снижение Δ_гр по сравнению с Δ_п будет, если все Δ_i,п одинаковы:

Δ_i,п =А.

При Р = 1 получим

Δ_п = ± nA,

а при Р < 1

Δ_гр = ± К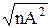= ± КА,

т.е.

=

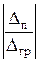например, при n = 4 и К = 1,1 различие между предельным и граничным значениями получается примерно в два раза.

Если, наоборот, какая-нибудь из Δ_i сильно преобладает над остальными, то

Δ_гр ≈ Δ_п.

 

Косвенные измерения.

Для вычисления погрешности мы располагаем известной функциональной зависимостью результата косвенного измерения Y от аргументов Х₁; Х₂;…Х_n:

Y = f (Х₁; Х₂;…Х_n).

Пример: R = здесь Y =R; Х₁ = U; X₂ = I.

Требуется найти погрешность ΔY, происходящую от погрешностей ΔХ₁; ΔХ₂;…ΔХ_n.

Упростим обозначения: ΔY = Δ; ΔХ₁ = Δ₁; ΔХ₂ = Δ₂;…ΔХ_n = Δ_n.

Для решения нашей задачи в математике есть т.н. «формула полного дифференциала»:

 

.

 

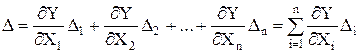Предельные значения Δ:

 

Р = 1.

 

Мы рассмотрели арифметическое суммирование при Р = 1. При Р < 1 применяют статистическое суммирование:

 

,

 

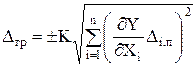где К зависит от задаваемого значения вероятности Р так же, как при прямых измерениях (см. табл. 1).

Каждый может написать формулы для Δ_гр для рассмотренных выше частных случаев.

 

Пример.

Требуется определить мощность Р, выделяющуюся в резисторе с номинальным значением сопротивления R_ном = 1 кОм с предельно допускаемыми отклонениями от этого номинала ± 1,0 %. Резистор подключён к источнику напряжения постоянного тока. Параллельно резистору постоянно подключён вольтметр класса точности 0,5 с диапазоном измерения от 0 до 15 В и он показывает значение напряжения U = 6,0 В.

Решение.(самостоятельно)