Задание 2. Построить математическую модель задачи и найти решение симплекс-методом.

№ варианта	Задание
	Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве 850, 1120, 1060единиц. При этом для продажи первой группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве 17 единиц, ресурса второго вида – в количестве 8 единиц, ресурса третьего вида – в количестве 4единиц. Для продажи второй и третьей групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве 5 и 5единиц, ресурсов второго вида – в количестве 6 и 6 единиц, ресурсов третьего вида – в количестве 2 и 4 единиц. Доход от продажи трех групп товаров на 1 тыс. руб. товарооборота составляет соответственно8, 7, 4 (тыс. руб.). Определите плановый объем и структуру товарооборота так, чтобы доход торгового предприятия был максимальным.
	Предприятие выпускает три вида изделий, причем суточный выпуск изделий составляет 90 ед. 1 вида, 70 ед. 2 вида и 60 ед. 3 вида. Суточные ресурсы следующие: производственное оборудование – 780 станко-ч, сырье – 850 кг, электроэнергия – 800 кВт. ч. Нормативы затрат оборудования, сырья и электроэнергии на ед. изделия представлены в таблице. Ресурсы Изделие Оборудование Сырье Эл. энергия Цена единицы изделий равна: 1 вида – 8 руб.; 2 вида – 7 руб.; 3 вида – 6 руб. Сколько нужно произвести изделий каждого вида, чтобы получить максимальный доход от выпуска изделий сверх плана?
	Производство трех видов продукции должно пройти две операции. Затраты времени на каждой операции на единицу продукции, прибыль от реализации единицы продукции, фонд времени на каждой операции даны в таблице. Продукция Затраты на единицу продукции Прибыль, руб. Операция 1 Операция 2 A B C Фонд времени   Сколько продукции каждого вида должно произвести предприятие, чтобы получить максимум прибыли, исходя из указанного в таблице фонда времени, если продукции А должно быть не менее 20 единиц.
	Цех выпускает три вида деталей – А, В, С. Каждая деталь обрабатывается тремя станками. Организация производства в цехе характеризуется следующей таблицей. Станок Длительность обработки детали, мин. Фонд времени, час. A B C I II III Отпускная цена за одну деталь   Определить план загрузки станков, обеспечивающий цеху получение максимальной прибыли.
	Нормы затрат на производство разных видов пиццы, объемы ресурсов и стоимость приведены в таблице. Продукты Нормы затрат на изготовление 100 шт. пиццы, кг Запасы продуктов, кг ассорти грибная салями Грибы Колбаса Тесто Цена за 1 шт., руб.   Определите оптимальное количество пиццы, обеспечивающее максимальный доход от продаж.
	На кондитерскую фабрику г. Покров перед Новым годом поступили заказы на подарочные наборы конфет из магазинов. Возможные варианты наборов, их стоимость и товарные запасы представлены в таблице. Наименование конфет Вес конфет в наборе, кг Запасы конфет, кг A B C Сникерс 0,3 0,2 0,4 Марс 0,2 0,3 0,2 Баунти 0,2 0,1 0,2 Цента, руб.   Определите оптимальное количество подарочных наборов, обеспечивающее максимальный доход от продажи.
	Металлургический цех выпускает три вида продукции: А, Б, В. Прибыль от тонны произведенной продукции каждого вида составляет соответственно 35, 25 и 40 руб. Цех располагает необходимым оборудованием, каждый тип которого имеет свой фонд рабочего времени и производительность. Тип оборудования Фонд времени, ч Производительность по видам продукции, т/ч А Б В Печь обжига Травильный агрегат 0,08 0,08 0,1 Прокатный стан 0,1 0,1 0,08 Составить план выпуска продукции, обеспечивающий максимум прибыли.
	Фирма выпускает три вида изделий. В процессе производства используются три технологические операции. 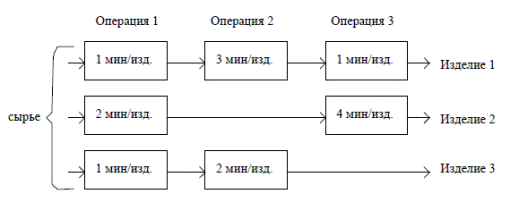  Фонд рабочего времени ограничен следующими предельными значениями: для первой операции – 430 мин; для второй операции – 460 мин; для третьей операции – 420 мин. Изучение рынка сбыта показало, что ожидаемая прибыль от продажи одного изделия видов 1, 2 и 3 составляет 3, 2 и 5 рублей соответственно. Построить наиболее выгодный суточный объем производства каждого вида продукции?
	Для реализации трех групп товаров коммерческое предприятие располагает тремя видами ограниченных материально-денежных ресурсов в количестве 180, 50, 40единиц. При этом для продажи первой группы товаров на 1 тыс. руб. товарооборота расходуется ресурса первого вида в количестве 3 единиц, ресурса второго вида – в количестве 2 единиц, ресурса третьего вида – в количестве 2единиц. Для продажи второй и третьей групп товаров на 1 тыс. руб. товарооборота расходуется соответственно ресурса первого вида в количестве 6 и 4единиц, ресурсов второго вида – в количестве 1 и 2 единиц, ресурсов третьего вида – в количестве 3 и 1 единиц. Доход от продажи трех групп товаров на 1 тыс. руб. товарооборота составляет соответственно 6, 5, 5 (тыс. руб.). Определите плановый объем и структуру товарооборота так, чтобы доход торгового предприятия был максимальным.
	Предприятие должно произвести три вида изделий (А, В, С) на двух видах оборудования, предназначенных соответственно для различных операций. Затраты времени (ч) на производство единицы изделий каждого вида, мощность оборудования и прибыль от реализации единицы продукции приведены в таблице. Изделие Оборудование Прибыль (руб.) А В С Мощность (маш.* ч.)   Сколько единиц изделий каждого вида надо произвести, чтобы получить максимум прибыли, если за простой единицы оборудования 1 вида берется штраф в количестве 1 руб./ч, а 2 вида – 0,5 руб./ч.

Задание 3. Составить диету включающие белки, жиры и углеводы в количестве не менее b_i (i = 1, 2, 3). Для составления смеси можно использовать три вида продуктов B_j (j = 1, 2, 3), содержащую белки жиры и углеводы в количестве a_ij. Цена продуктов C_j. Необходимо определить такой набор продуктов, который обеспечил бы необходимое содержание питательных веществ, и полная стоимость его при этом была бы наименьшей.

Требуется:

1) составить математическую модель прямой и двойственной задач; раскрыть экономический смысл всех переменных, принятых в задаче;

2) симплекс-методом решить двойственную задачу;

3) найти решение исходной задачи с использование теорем двойственности.

Параметр	Номер варианта
b1
b2
b3
а11
а12
а13
а21
а22
а23
а31
а32
а33
С1
С2
С3

Задание 4. В пунктах А_i (i = 1, 2, 3) производится однородная продукция в количестве а_i единиц. Себестоимость единицы продукции в i-м пункте равна C_i. Готовая продукция поставляется в пункты В_j (j = 1, 2, 3, 4), потребности которых составляют b_j ед. стоимость перевозки единицы продукции из пункта A_i в пункт B_j задана матрицей C_ij.

Требуется:

1) написать математическую модель прямой и двойственной задач с указанием экономического смысла всех переменных;

2) составить план перевозки продукции, при котором минимизируются суммарные затраты по ее изготовлению и доставке потребителям для условия что продукция произведенная в пункте A_i,где себестоимость её производства наименьшая, распределяется полностью;

3) вычислить суммарные минимальные затраты Z_min;

4) узнать в какие пункты развозится продукция от поставщиков;

4) установить пункты, в которых останется нераспределенная продукция, и указать её объем.

Параметр	Номер варианта
а1
а2
а3
С1
С2
С3
b1					296
b2
b3
b4
С11
С12
С13
С14
С21
С22
С23
С24
С31
С32
С33
С34

Задание 5. Выделены денежные средства S₀=100 д.ед. для вложения в инвестиционные проекты для реконструкции и модернизации производства на четырех предприятиях.

По каждому предприятию известен возможный прирост f_i(х) (i=1, 2, 3, 4) выпуска продукции в зависимости от выделенной суммы.

Требуется: 1) распределить средства S₀ между предприятиями так, чтобы суммарный прирост продукции на всех четырех предприятиях достиг максимальной величины;

2) используя решение основной задачи, найти оптимальное распределение между тремя предприятиями.