Их произведение равно 1, а, следовательно, по предположению индукции

х1+х2+…+хk-1+xkxk+1³k.

Прибавим к обеим частям последнего неравенства xk + xk+1, перенесем xkxk+1 направо и преобразуем правую часть неравенства:

х1+х2+…+хk+xk+1³k - xkxk+1+ xk + xk+1=k+1+xk(1- xk+1)+ xk+1-1= k+1+(1- xk+1) (xk-1)³k+1.

Таким образом, из истинности утверждения при n=k вытекает его истинность при n=k+1.

ПРИМЕР 3. Докажите, что число Аn=10n+18n-28 кратно 27 для всех натуральных n.

Доказательство. 1. При n =1, А1=0, очевидно, кратно 27.

1. Пусть Аn кратно 27 при n = k, и докажем делимость Аn при n = k+1.

Имеем Аk+1=10k+1 + 18(k+1) - 28 =10Ak - 162k + 270 = 10Ak + 27(10 - 6k), что доказывает делимость на 27. На основании метода математической индукции, заключаем, что Аn кратно 27 при любом натуральном n.

Рассмотрим некоторые обобщения принципа математической индукции.

Пусть р - некоторое целое число.

Предложение А(к), где к целое, истинно для всех целых значений к³р, если выполнены следующие два условия:

1) Предложение А(к) истинно для к=р.

2) Из предположения, что А(к) истинно для к=n (n - целое, n ³р), следует, что оно верно для следующего значения к=n + 1.

ПРИМЕР 4. Доказать, что любую сумму денег, большую 7 копеек, можно разменять трехкопеечными и пятикопеечными монетами.

Доказательство. Пусть сумма равна n копейкам. Если n = 8, то утверждение верно. Пусть утверждение верно для n=к. Могут представиться только два случая для размена суммы в к копеек.

а) потребовались только трехкопеечные монеты,

б) потребовалась хотя бы одна пятикопеечная монета.

В случае а) удаляем три трехкопеечные монеты и добавляем две пятикопеечные и тем самым размениваем сумму в к+1 копеек. В случае б) удаляем одну пятикопеечную монету и добавляем две трехкопеечные и тем самым размениваем сумму в к+1 копеек.

Приведем пример применения метода математической индукции в геометрии.

ПРИМЕР 5. Докажите, что количество диагоналей выпуклого к-угольника подсчитывается по формуле, где

Доказательство. Очевидно, формула верна при n=4. Предположим, что она верна и в случае n-угольника и докажем ее для (n+1)-угольника. Рассмотрим (n+1)-угольник A1A2…AnAn+1. Проведем отрезок AnA1. Он разобьет наш (n+1)-угольник на n-угольник A1A2…An и треугольник AnA1Аn+1. Тогда количество диагоналей n-угольника A1A2…An равно и к ним еще прибавятся диагонали, которые получаются соединением вершины Аn+1 с вершинами A2, A3, … , An-1 и диагональ AnA1, т.е. добавится n-1 диагональ. Но тогда их общее количество будет равно На основании метода неполной математической индукции заключаем, что формула верна для любого выпуклого n-угольника.

 

Доказательство теоремы 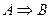называется синтетическим, если оно проводится по следующей логической схеме

где Т – определенная совокупность утверждений той математической теории в рамках которой и происходит доказательство данного предложения и которой принадлежит конечная последовательность предложений С1, С2, …, Сn, составляющих доказательство, а также суждения А и В.

Значит, доказательство теоремы 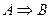синтетическим методом начинается с получения некоторого следствия С1 из условия теоремы А, или части условия теоремы и положений теории Т, истинность которых известна. Затем аналогично получают следующее следствие С2 и т.д. до тех пор, пока из последнего полученного следствия Сn легко получаем вывод заключения теоремы В.

Данный способ доказательства обладает как недостатками, так и достоинствами. К недостаткам следует отнести большую степень неопределенности в процессе проведения доказательства, что порождает у школьников чувство искусственности при проведении такого доказательства. Даже если школьники и слушают излагаемое учителем синтетическое доказательство, то для них мотивы предпринимаемых шагов остаются, как правило, скрытыми до завершения доказательства. Это обстоятельство и затрудняет обучение доказательству теорем школьников синтетическим методом. Им непонятно, почему берется именно эта, а не какая-то другая часть условия теоремы; почему вводятся в доказательство именно эти дополнительные предложения и понятия; почему выводится именно это следствие на данном этапе, а не другое. И только в конце доказательства все становится на свои места.

К достоинствам следует отнести лаконичность изложения доказательства, поэтому этот метод доказательства теорем и преобладает в учебниках при изложении доказательств.

Рассмотрим пример доказательства синтетическим методом и снабдим их комментариями.

ПРИМЕР 1. Известно, что Докажите, что

Доказательство. Рассмотрим очевидное неравенство (Почему именно это неравенство, а не другое?)

Перепишем это неравенство следующим образом: (Почему именно так, а не иначе?)

Добавим к обеим частям последнего неравенства Получим 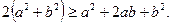(Зачем?)

Заменим в левой части (Почему не в правой?) на 1, получим, 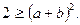Извлекая квадратный корень из обеих частей, получим

Неравенство доказано.

 

Доказательство теоремы методом восходящего анализа происходит по следующей схеме. Отправляясь от заключения, подбирают для него достаточное условие, т.е. такое суждение В1, что , затем подбирают достаточное условие В2 для В1, т.е. - истинно, и т.д. до тех пор, пока не получат такое достаточное условие Вn для Вn-1, что Вn истинно и легко следует из условий теоремы и некоторой совокупности Т связанных с А и С предложений данной теории. Символически процесс рассуждения по методу восходящего анализа может быть изображен так:

 

Такое доказательство является строгим и логичным, однако оформление такого доказательства лучше обратить и записать в синтетическом виде:

хотя в этом нет большой необходимости. Рассмотрим пример доказательства неравенства предыдущего пункта методом восходящего анализа.

Наше неравенство легко следует из неравенства 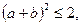которое в свою очередь легко получается из неравенства или 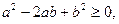которое очевидно.

 

Нисходящим анализом называют такую разновидность доказательства, при котором, отправляясь от заключения С доказываемого предложения 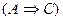, рассуждения ведут путем последовательного получения логических следствий

где Вn такое предложение, истинность которого уже доказана. При этом рассуждении предполагается, что утверждение С истинно.

Однако, при применении нисходящего анализа следует иметь в виду, что возможны следующие два принципиально различные случая:

1. Полученное следствие Вn ложно. В этом случае получаем, что и утверждение С ложно.

2. Полученное следствие Вn истинно. В этом случае ничего нельзя сказать об истинности доказываемого предложения С. Это объясняется тем, что из ложного суждения можно получить и истинное утверждение. Пример: 2= -2 – ложно, однако 4=4 – истинно. Поэтому в таком случае следует попытаться обратить этот процесс доказательства в синтетическое:

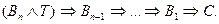
Если это удалось осуществить, то требуемое утверждение доказано синтетическим методом, а нисходящий анализ подсказал только путь нахождения такого доказательства. Если же обращение не удалось, то утверждение остается недоказанным и нужно искать другой способ доказательства. На последнее обстоятельство нужно особо обращать внимание учащихся, ибо именно на этом месте очень много совершается ошибок. Рассмотрим следующий пример.

ПРИМЕР. Доказать неравенство

(*)

где x и y – положительные числа.

Очень часто приходится слышать от школьников такое «доказательство».

Из неравенства (*) следует, что

или

откуда

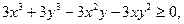
т.е.

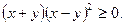
Последнее неравенство, очевидно, выполняется, а значит требуемое неравенство доказано.

В такой ситуации следует разъяснять учащимся ошибочность их рассуждений, причем делать это надо на конкретных примерах.

 

Доказательство противоречием школьникам хорошо известно под названием «доказательство от противного». Этот метод достаточно широко распространен в школьном курсе, особенно при доказательстве обратных теорем.

Общая схема доказательства противоречием описывается так. Пусть доказывается теорема Предположим, что С ложно. Тогда по закону исключения третьего, получаем, что будет истинным противоположное суждение . Получаем теорему . Путем нисходящего анализа приходим от к Вn. Пусть последнее утверждение противоречит ранее установленным фактам. Отсюда делаем вывод, что суждение так же ложно, а значит истинно противоположное С.

Отдельным пунктом поговорим об обратных теоремах. Как известно, если верна теорема 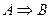, то обратная верна не всегда, а потому требует отдельного доказательства. Как правило, такие теоремы доказываются методом от противного. Приведем пример одной из таких теорем.

ТЕОРЕМА. Если через вершину треугольника АВС проходит прямая КМ так, что она образует угол со стороной ВС равный углу САВ и не пересекает строну АС треугольника, то эта прямая является касательной к окружности, описанной около треугольника АВС.

Доказательство. Опишем около треугольника АВС окружность и предположим противное, т.е. что данная прямая КМ не является касательной к этой окружности. Но тогда существует прямая l, отличная от КМ и проходящая через точку В, которая является касательной к этой окружности. По теореме об угле между касательной и хордой, получаем, что угол между прямой l и стороной ВС равен углу ВАС, т.е. он равен углу МВС. Но тогда прямая l должна совпадать с прямой КМ, что приводит к противоречию. Теорема доказана.

Данная теорема не рассматривается в школьном курсе математики, однако встречается ряд задач, где ее применение позволяет проще изложить решение.

Однако не всегда можно доказывать обратные теоремы. Это позволяет избежать следующая логическая теорема.
ТЕОРЕМА. Если верна совокупность предложений

(1)

где А1,…,Аn единственно возможны, полностью исчерпывают все возможные случаи условия, разделены по определенному признаку, а В1,…,Вn различны и несовместимы одно с другим, то верна совокупность соответствующих обратных предложений

(2)

Доказательство. Допустим, что одно из утверждений (2) имеет вид где 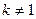, хотя совокупность (1) удовлетворяет всем перечисленным условиям. Но тогда т.к. получим что противоречит несовместимости В1 и Вk. Теорема доказана.

Как следствие этой теоремы получаем три геометрические теоремы для квадрата стороны треугольника, лежащей соответственно против прямого, острого или тупого угла. Эти теоремы удовлетворяют всем требованиям совокупности (1), а потому верны и обратные к ним теоремы, т.е. если в треугольнике:

1) 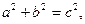то угол С прямой;

2) то угол С острый;

3) то угол С тупой.

Хотя обращение по разделению в общем виде на уроках не рассматривается, однако учитель в приведенном здесь и подобных конкретных случаях должен говорить о существовании обратных теорем и вводить их в обиход. Это позволит избежать логической ошибки, когда, например, при определении вида треугольника ссылаются на прямые теоремы, и, в частности, на теорему Пифагора.

 

При изучении доказательств теорем в школьном курсе математики преследуется две цели. Первая из них состоит в том, чтобы учащиеся хорошо усвоили изучаемые теоремы, а вторая – научить учащихся самостоятельно доказывать различные теоремы. Отсюда вытекает важное требование к изучению теорем, которое состоит в том, чтобы учитель не преподносил все доказательства теорем в готовом виде и не требовал от школьников только заучиванию готовых доказательств.

При обучении школьников доказательству теорем учителю рекомендуется придерживаться следующих правил:

1) Перед доказательством теоремы следует восстановить в памяти учащихся тот ранее изученный материал, который будет использоваться при доказательстве.

2) Перед тем как приступать к доказательству новой теоремы учитель обязан убедиться, что каждый ученик понял ее содержание, четко определил ее условие и заключение.

3) При доказательстве теорем всегда подчеркивать вспомогательную роль чертежа, но требовать от ученика делать чертеж аккуратно и как можно более близко к данным теоремы.

4) При доказательстве теорем требовать от учеников применение только тех фактов и теорем, истинность которых либо хорошо известна, либо была установлена ранее. Интуиция и всевозможные догадки здесь должны играть лишь вспомогательную роль при поиске хода доказательства.

5) Перед тем как приступать к доказательству теоремы учитель обязан хорошо мотивировать изучение этой теоремы, чтобы возникла «потребность» в изучении теоремы.

6) При обучении доказательству теорем учителю следует ознакомить учащихся со следующими правилами доказательства.

А) Условие теоремы преобразуется с целью сближения с заключением.

В) Заключение теоремы преобразуется с целью сближения с условием.

Г) Определяемое понятие в условии или заключении теоремы или появляющееся в доказательстве, заменяется его определением.

Д) При наличии нескольких определений понятия используется то, которое сокращает путь доказательства.

Е) Вместо определения понятия используется его признак.

Ж) Условие теоремы используется полностью.

Остановимся кратко на этих требованиях.

Повторение ранее изученного материала, необходимого на данном уроке, может проходить по-разному. Можно просто задать повторить тот или иной материал, можно дать задачу на применение именно такого материала. Однако проверка того, как учащиеся повторили этот материал, необходима перед доказательством теоремы и проводить это можно так же в различной форме: начиная от устного опроса до проведения краткой самостоятельной работы по этому материалу. В процессе же доказательства можно просто ограничиться ссылками на этот материал, однако ссылки должны быть полными и обоснованными.

При доказательстве теоремы чертеж играет вспомогательную роль, однако правильно выполненный чертеж иногда подсказывает путь доказательства теоремы. Кроме этого роль чертежа как наглядного пособия оказывает большую роль при изучении доказательства. Если чертеж сделан красиво, на нем выделены основные элементы, играющие роль при доказательстве, то при воспроизведении доказательства ученик будет лучше ориентироваться. В этом отношении замечателен опыт работы Шаталова по своим так называемым «опорным конспектам».

Мы с вами уже отмечали роль мотивации в обучении. Она состоит в том, чтобы вызвать осознанную потребность и интерес в изучении материала. Этого можно достичь разными методами, и в этом отношении наработан большой запас различных приемов. Хорошо известен метод занимательных и целесообразных задач. Можно рассмотреть исторические факты, связанные с данным материалом. Однако одно из основных требований в изучении новой теоремы состоит в том, чтобы ее изучение довести до рассмотрения конкретных примеров, на которых видно применение данной теоремы или утверждения.

В отношении правил доказательства следует отметить необходимость как можно раньше ознакомить учащихся с данными правилами, чтобы учащиеся записали их и затем применяли. Можно вывесить плакат с этими правилами на тех уроках, где будут доказываться теоремы.

В заключение отметим, что, как правило, после доказательства теорем при решении задач используются лишь формулировки теорем. Это приводит учащихся к мысли, что самое важное в теореме – ее формулировка, а все остальное можно не учить. К сожалению, программа по математике в базовом классе приучает учеников к такой мысли более активно. Поэтому следует иногда повторять доказательство той или иной теоремы, а при решении задач в математическом классе, когда ученики пытаются использовать материал выходящий за рамки школьного курса (особенно при решении нестандартных задач), следует требовать от них осознанного применения этих теорем, т.е. чтобы школьники приводили и доказательство этих теорем. Это особенно важно в старших классах, когда идет подготовка к поступлению в вуз, где на вступительных экзаменах требуется доказательство всех фактов выходящих за рамки школьной программы. Поэтому теоремы, рассмотренные на факультативах и занятиях кружка, следует также доказывать.