Исследование переходных процессов методом дифференциальных уравнений
Получение в линеаризованном виде дифференциальных уравнений описывающих поведение динамической системы при действии на нее возмущающих факторов, является первым и необходимым этапом на пути решения задачи анализа действующей системы управления, осуществляемой с целью исследования возможности достижения наиболее качественной работы системы, характеризуемой тем или иным критерием оптимальности. В частности, о качестве системы управления можно судить по виду переходного процесса, определяемому значениями постоянных коэффициентов линейных дифференциальных уравнений.
Выше отмечалось, что для линейной динамической системы связь между входом и выходом определяется линейным дифференциальным уравнением вида:
, (1-10)
где y(t) и x(t) – соответственно выход и вход системы,
an…a0; bm…b0 – постоянные коэффициенты.
Из теории дифференциальных уравнений известно, что решение уравнения вида (1-10) представляет собой сумму свободной и вынужденной составляющих:
(1-11)
легко определяемых при заданных начальных условиях и известной величине входного воздействия.
Свободная составляющая решения – yсв(t) является общим решением уравнения (1-10) без правой части:
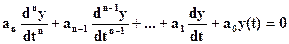, (1-12)
которое ищется в одном из следующих видов.
1. Если корни характеристического уравнения, получаемого из уравнения (1-12) заменой 
на оператор P:
(1-13)
будут действительными и различными, то свободная составляющая определяется выражением:
,
где ck – произвольные постоянные, определяемые начальными условиями;
Pk – корни характеристического уравнения;
t – текущее значение времени.
2. Если характеристическое уравнение имеет корень Pk кратности e, то соответствующая этому корню свободная составляющая определяется из выражения:
.
3. Если характеристическое уравнение имеет пару комплексно-сопряженных корней (
; 
), то решение свободной составляющей ищется в виде:
.
Вынужденная составляющая решения дифференциального уравнения характеризует собой установившейся режим работы системы и называется также установившейся составляющей, зависящей от вида функции x(t).
Свободная составляющая существует только в переходных и в устойчивых системах (т.е. системах, возвращающихся в первоначальное состояние после нанесения возмущения) со временем исчезает, поэтому ее называют также переходной составляющей или переходным процессом. Свободная составляющая совершенно не зависит от вида функции x(t), но всецело определяется внутренними свойствами самой системы.
При исследовании систем автоматического управления часто вместо исходных линейных дифференциальных уравнений с постоянными коэффициентами целесообразно переходить к алгебраической форме дифференциальных уравнений, которая является более универсальной и существенно облегчает теоретические исследования динамических систем. Для осуществления алгебраизации дифференциальных уравнений используется метод операционного исчисления, заключающийся в том, что в общем случае решение исходной системы линейных дифференциальных уравнений для оригиналов заменяется решением системы алгебраических уравнений для изображений. В этом случае дифференциальное уравнение (10) может быть записано также в операторном или символическом виде:
, (1 – 14)
где 
- символ дифференцирования;
Y(p) и X(p) – изображение выходной и входной величины.
Последнее выражение может быть формально представлено в виде:
. (1-15)
Обозначив
, (1-16)
получим удобную форму записи уравнения (1-10):
. (1-17)
Здесь функция W(p) называется передаточной функцией системы и представляет собой отношение изображение выхода к изображению входа.
Таким образом, решение уравнения (1-17), представляющего собой операторную форму записи линейного дифференциального уравнения с постоянными коэффициентами, сводится к следующему.
По таблице изображений находится изображение входной величины, которое в общем случае связано с действительным значением входа интегралом:
, (1-18)
где p – комплексная переменная.
В результате алгебраического перемножения изображения входной величины и передаточной функции системы находится изображение выходной величины – Y(p). По таблицам изображений находится оригинал (действительное значение) выходной величины, в общем случае связанный с изображением интегралом:
. (1-19)
Полученное в результате последней операции нахождения оригинала по его изображению значение выхода – y(t) и есть решение исходного дифференциального уравнения.
Пример: Необходимо найти переходный процесс в системе, преобразующей входное воздействие в соответствии с дифференциальным уравнением (1-9):
, (а)
где x(t) – вход;
y(t) – выход;
T – постоянная времени системы;
K – коэффициент усиления системы.
Полагая, что на вход системы подается единичное ступенчатое воздействие 
, при нулевом начальном значении Y0=0 и t>0 имеем следующее уравнение:
. (б)
Для нахождения свободной составляющей решения запишем характеристическое уравнение, имеющее вид:
. (в)
Так как характеристическое уравнение имеет один корень 
, то свободная составляющая решения находится в виде:
,
где c – произвольная постоянная;
t – текущее значение времени;
T – постоянная времени системы.
Вынужденную составляющую уравнения (б) будем искать в виде постоянной величины Yвых(t)=A, так как правая часть исходного дифференциального уравнения есть величина постоянная. Тогда уравнение (б) запишется в виде:
,
характеризующем установившийся режим работы системы. Таким образом, общее решение уравнения (б) определяется выражением:
(г)
в котором неизвестной является лишь произвольная постоянная c , которую можно найти, зная начальные условия. В данном случае начальное отклонение выхода должно отсутствовать, так как в правой части уравнения (а) производные отсутствуют, и следовательно, начальными условиями для решения уравнения (б) являются:
t=0 и y(t)=0.
Подставив начальные условия в уравнение (г), получим:
,
Откуда находится произвольная постоянная c:
.
Подставив произвольную постоянную в уравнение (г), находим окончательное решение дифференциального уравнения системы:
.
Зная коэффициенты уравнения и, подставляя в него текущее значение времени, можно найти переходный процесс в системе, имеющий вид, представленный на рис. 1 – 11.
