Линейное однородное уравнение.
Рассмотрим линейное уравнение без правой части:
 . (3.1)
. (3.1)
Через  мы будем сокращенно обозначать результат применения к функции
мы будем сокращенно обозначать результат применения к функции  совокупности операций [дифференцирование, умножение на функции
совокупности операций [дифференцирование, умножение на функции  и сложение], указываемых левой частью уравнения (3.1), и будем называть
и сложение], указываемых левой частью уравнения (3.1), и будем называть  линейным дифференциальным выражением или линейным дифференциальным оператором. Линейный оператор обладает следующими двумя важными свойствами:
линейным дифференциальным выражением или линейным дифференциальным оператором. Линейный оператор обладает следующими двумя важными свойствами:
1)  , (6)
, (6)
где  — любые функции, имеющие
— любые функции, имеющие  непрерывных производных. В самом деле, раскрывая значения символа оператора, имеем
непрерывных производных. В самом деле, раскрывая значения символа оператора, имеем
 Оператор от суммы равен сумме операторов слагаемых. Это свойство доказано для суммы двух слагаемых, но оно, очевидно, распространяется на сумму любого числа слагаемых.
Оператор от суммы равен сумме операторов слагаемых. Это свойство доказано для суммы двух слагаемых, но оно, очевидно, распространяется на сумму любого числа слагаемых.
2)  , (7)
, (7)
где  — любая
— любая  раз дифференцируемая функция, а
раз дифференцируемая функция, а  — постоянная, т.е. постоянный множитель можно вынести за знак линейного оператора. Доказательство легко проводится подобно предыдущему случаю. На основании свойств линейного оператора, выражаемых тождествами (6) и (7), получаются следующие теоремы о решениях однородного линейного уравнения.
— постоянная, т.е. постоянный множитель можно вынести за знак линейного оператора. Доказательство легко проводится подобно предыдущему случаю. На основании свойств линейного оператора, выражаемых тождествами (6) и (7), получаются следующие теоремы о решениях однородного линейного уравнения.
Теорема 1. Если  и
и  есть два (частных) решения уравнения (3.1), то
есть два (частных) решения уравнения (3.1), то  есть также решение этого уравнения.
есть также решение этого уравнения.
Доказательство. Так как  есть решения, то имеем тождества
есть решения, то имеем тождества  . Но, в силу (6),
. Но, в силу (6),  , что, в силу условия, равно нулю тождественно. Теорема доказана.
, что, в силу условия, равно нулю тождественно. Теорема доказана.
Теорема 2. Если  есть решение уравнения (3.1), то
есть решение уравнения (3.1), то  есть также решение этого уравнения (
есть также решение этого уравнения ( — любая постоянная).
— любая постоянная).
Доказательство. В силу свойства (7),  , а по условию
, а по условию  , откуда и следует теорема.
, откуда и следует теорема.
Следствие 1. Если имеем частные решения уравнения (3.1)  , то выражение
, то выражение  есть также решение этого уравнения (
есть также решение этого уравнения ( — любые постоянные).
— любые постоянные).
Следствие 2. Если  есть частные решения линейного однородного уравнения
есть частные решения линейного однородного уравнения  -го порядка, то выражение
-го порядка, то выражение
 (8)
(8)
есть решение, содержащее  произвольных постоянных, т.е. общее решение.
произвольных постоянных, т.е. общее решение.
Следует отметить, что всякое линейное однородное уравнение имеет частное решение  . Это решение называется тривиальным. В теории интегрирования мы его учитывать не будем.
. Это решение называется тривиальным. В теории интегрирования мы его учитывать не будем.
Вопрос о том, каким условиям должны удовлетворять частные решения, чтобы выражение (8) являлось общим решением однородного уравнения, разрешается в связи с понятием линейной зависимости функций. Функции  , определенные на интервале
, определенные на интервале  , называются линейно зависимыми на этом интервале, если существуют постоянные
, называются линейно зависимыми на этом интервале, если существуют постоянные  , не все равные нулю, такие, что для всех значений
, не все равные нулю, такие, что для всех значений 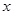 на рассматриваемом интервале выполняется тождественно соотношение
на рассматриваемом интервале выполняется тождественно соотношение
 . (9)
. (9)
Если не существует таких постоянных, чтобы равенство (9) имело место для всех рассматриваемых значений 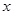 (не всех равных нулю), то функции называются линейно независимыми (на данном интервале). В последующем мы часто будем иметь дело с интервалом
(не всех равных нулю), то функции называются линейно независимыми (на данном интервале). В последующем мы часто будем иметь дело с интервалом  .
.
Рассмотрим один частный случай и несколько примеров.
1) Если одна из функций, например  , равна на данном интервале нулю, то все функции линейно зависимы, так как мы имеем тождество
, равна на данном интервале нулю, то все функции линейно зависимы, так как мы имеем тождество  , в котором можно взять
, в котором можно взять  .
.
2) Функции  линейно независимы на интервале
линейно независимы на интервале  , а также
, а также
на любом конечном интервале. Допустив противное, мы получили бы равенство  для всех рассматриваемых значений
для всех рассматриваемых значений 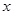 (не все
(не все  равны нулю). Между тем написанное равенство есть алгебраическое уравнение степени не выше
равны нулю). Между тем написанное равенство есть алгебраическое уравнение степени не выше  ; оно может быть справедливым не более как для
; оно может быть справедливым не более как для  значений
значений 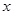 .
.
3) Пусть  — любые действительные не равные между собой числа,
— любые действительные не равные между собой числа,  . Тогда функции, определенные для
. Тогда функции, определенные для  ,
,  линейно независимы. Допустим противное; пусть имеет место тождество
линейно независимы. Допустим противное; пусть имеет место тождество  для всех значений
для всех значений  . Умножая предполагаемое тождество на
. Умножая предполагаемое тождество на  , получим тождество
, получим тождество  . Замечая, что все показатели больше нуля, получим предельным переходом при
. Замечая, что все показатели больше нуля, получим предельным переходом при  , что необходимо
, что необходимо  . Поэтому тождество может иметь только такой вид:
. Поэтому тождество может иметь только такой вид:  . Повторяя последовательно то же рассуждение, получим
. Повторяя последовательно то же рассуждение, получим  , т.е. противоречие с предположением, что не все
, т.е. противоречие с предположением, что не все  равны нулю. Это противоречие доказывает наше утверждение. Такое же рассуждение можно было применить и к предыдущему примеру.
равны нулю. Это противоречие доказывает наше утверждение. Такое же рассуждение можно было применить и к предыдущему примеру.
4) Примером линейно зависимой системы являются функции  . Действительно, полагая
. Действительно, полагая  получаем тождество для
получаем тождество для  :
:  .
.
Пусть мы имеем  функций от
функций от 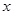 , имеющих непрерывные производные до
, имеющих непрерывные производные до  -го порядка:
-го порядка:  .
.
Определитель
 (10)
(10)
называется определителем Вронского этих функций. Легко доказывается следующая теорема.
Теорема 3. Если функции  линейно зависимы, то определитель Вронского тождественно равен нулю.
линейно зависимы, то определитель Вронского тождественно равен нулю.
Пусть функции  линейно зависимы, т.е. существует тождественное соотношение
линейно зависимы, т.е. существует тождественное соотношение
 , (11)
, (11)
где не все  равны нулю. Без ограничения общности мы можем допустить, что
равны нулю. Без ограничения общности мы можем допустить, что  (иначе мы изменили бы нумерацию функций). Выражая из соотношения (11)
(иначе мы изменили бы нумерацию функций). Выражая из соотношения (11)  , получаем тождество
, получаем тождество
 , (11.1)
, (11.1)
где  . Из тождества (11.1) дифференцированием по
. Из тождества (11.1) дифференцированием по 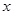 получаем
получаем
 (11.2)
(11.2)
Умножаем в выражении (10) первый столбец на  , второй на
, второй на  , …,
, …,  -й на
-й на  и прибавляем к последнему. Величина определителя
и прибавляем к последнему. Величина определителя  не изменится, но в силу соотношений (11.1) и (11.2) последний столбец нового определителя будет состоять из нулей, откуда следует, что
не изменится, но в силу соотношений (11.1) и (11.2) последний столбец нового определителя будет состоять из нулей, откуда следует, что  , что и требовалось доказать.
, что и требовалось доказать.
Если  есть частные решения однородного уравнения (3.1), то справедлива обратная, причем более сильная теорема.
есть частные решения однородного уравнения (3.1), то справедлива обратная, причем более сильная теорема.
Теорема 4. Если решения  линейно независимы (на интервале (2)), то
линейно независимы (на интервале (2)), то  не обращается в нуль ни в одной точке рассматриваемого интервала.
не обращается в нуль ни в одной точке рассматриваемого интервала.
Допустим противное. Пусть  . Обозначим величины
. Обозначим величины  при
при  через
через  и значения
и значения  через
через  и составим систему уравнений
и составим систему уравнений
 (12)
(12)
Рассматривая в уравнениях (12) величины  как неизвестные, мы получим для определителя системы (12) значение
как неизвестные, мы получим для определителя системы (12) значение  . Следовательно, однородная система (12) из
. Следовательно, однородная система (12) из  уравнений с
уравнений с  неизвестными имеет систему решений
неизвестными имеет систему решений  , причем не все
, причем не все  равны нулю. Составим функцию
равны нулю. Составим функцию
 . (8.1)
. (8.1)
В силу следствия 1 теорем 1 и 2 она является решением уравнения (3.1). В силу условий (12), мы имеем при 
 . (12.1)
. (12.1)
Начальные условия (12.1) по теореме существования определяют единственное решение уравнения (3.1). Но таким решением, очевидно, является тривиальное решение  , следовательно,
, следовательно,  на интервале
на интервале  , и мы получаем из равенства (8.1)
, и мы получаем из равенства (8.1)  для любого
для любого 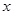 на интервале (2), причем не все
на интервале (2), причем не все  равны нулю, т.е. функции
равны нулю, т.е. функции  линейно зависимы вопреки предположению. Полученное противоречие доказывает теорему.
линейно зависимы вопреки предположению. Полученное противоречие доказывает теорему.
Теоремы 3 и 4 можно объединить в следующей формулировке: определитель Вронского, составленный для системы  решений линейного уравнения
решений линейного уравнения  -го порядка (3.1), или тождественно равен нулю, или не обращается в нуль ни в одной точке того интервала, где коэффициенты уравнения непрерывны.
-го порядка (3.1), или тождественно равен нулю, или не обращается в нуль ни в одной точке того интервала, где коэффициенты уравнения непрерывны.
Любая система из  линейно независимых частных решений линейного однородного уравнения (3.1) называется фундаментальной системой.
линейно независимых частных решений линейного однородного уравнения (3.1) называется фундаментальной системой.
Следствие теоремы 4. Функции, образующие фундаментальную систему, линейно независимы во всяком частичном интервале  , содержащемся в
, содержащемся в  . Это следует из необращения в нуль определителя Вронского.
. Это следует из необращения в нуль определителя Вронского.
Теорема 5. Для всякого дифференциального уравнения существует фундаментальная система.
В самом деле, возьмем любую систему таких  чисел
чисел  (
( ), такую, чтобы составленный из них определитель
), такую, чтобы составленный из них определитель
 (13)
(13)
был отличен от нуля. Определим  частных решений
частных решений  уравнения (3.1) начальными условиями: при
уравнения (3.1) начальными условиями: при  имеем
имеем  . Функции определены на всем интервале (2).
. Функции определены на всем интервале (2).
Определитель (13) представляет собой значение определителя Вронского  при
при  . Таким образом,
. Таким образом,  заведомо не равен нулю при
заведомо не равен нулю при  , откуда, в силу теоремы 3, следует, что
, откуда, в силу теоремы 3, следует, что  линейно независимы, т.е. образуют фундаментальную систему (вспомним, что
линейно независимы, т.е. образуют фундаментальную систему (вспомним, что  не равен нулю ни для какого
не равен нулю ни для какого 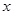 в интервале
в интервале  ).
).
Матрицу  с определителем (13), отличным от нуля, часто бывает полезно выбрать по следующему закону:
с определителем (13), отличным от нуля, часто бывает полезно выбрать по следующему закону:  , когда
, когда  ,
,  при
при  . Очевидно, определитель (13) равен в этом случае единице. Соответствующую фундаментальную систему
. Очевидно, определитель (13) равен в этом случае единице. Соответствующую фундаментальную систему  мы будем называть нормальной фундаментальной системой. Составляющие эту систему функции удовлетворяют таким начальным условиям: при
мы будем называть нормальной фундаментальной системой. Составляющие эту систему функции удовлетворяют таким начальным условиям: при 

Теорема 6. Если  образуют фундаментальную систему решений уравнения
образуют фундаментальную систему решений уравнения  , то общее решение выражается формулой
, то общее решение выражается формулой
 . (8)
. (8)
По определению, решение, содержащее  произвольных постоянных, называется общим, если из него при определенных числовых значениях постоянных получается любое частное решение. А как было указано, в силу теоремы существования и единственности, любое частное решение однозначно определяется начальными условиями: при
произвольных постоянных, называется общим, если из него при определенных числовых значениях постоянных получается любое частное решение. А как было указано, в силу теоремы существования и единственности, любое частное решение однозначно определяется начальными условиями: при 
 , (14)
, (14)
где  — любые числа, и
— любые числа, и  . Мы докажем, что решение (8) есть общее, если покажем, что можно в формуле (8) определить постоянные
. Мы докажем, что решение (8) есть общее, если покажем, что можно в формуле (8) определить постоянные  так, чтобы удовлетворялись условия (14). Для определения постоянных
так, чтобы удовлетворялись условия (14). Для определения постоянных  мы получаем систему линейных уравнений
мы получаем систему линейных уравнений
 (15)
(15)
Здесь  обозначает значение функции
обозначает значение функции  при
при  ;
;  есть значение производной
есть значение производной  при
при  . Определитель системы (15) есть определитель Вронского, в котором вместо
. Определитель системы (15) есть определитель Вронского, в котором вместо 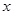 подставлено
подставлено 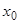 , т.е.
, т.е.  . В силу теоремы 4,
. В силу теоремы 4,  . Следовательно, система уравнений (15) всегда допускает, и притом единственную, систему решений
. Следовательно, система уравнений (15) всегда допускает, и притом единственную, систему решений  . Выражение (8), в котором
. Выражение (8), в котором  имеют полученные таким образом значения, очевидно, удовлетворяет начальным условиям (14). Теорема доказана.
имеют полученные таким образом значения, очевидно, удовлетворяет начальным условиям (14). Теорема доказана.
Если  представляет собой нормальную фундаментальную систему, то решение, удовлетворяющее начальным условиям (14), получает простую форму
представляет собой нормальную фундаментальную систему, то решение, удовлетворяющее начальным условиям (14), получает простую форму  . В справедливости этого утверждения можно убедиться, подставляя в него и в выражения, полученные из него последовательным дифференцированием, значение
. В справедливости этого утверждения можно убедиться, подставляя в него и в выражения, полученные из него последовательным дифференцированием, значение  .
.
Пример 1. Уравнение  имеет, как легко проверить, два частных решения:
имеет, как легко проверить, два частных решения:  . Для выяснения вопроса об их линейной зависимости или независимости составляем определитель Вронского:
. Для выяснения вопроса об их линейной зависимости или независимости составляем определитель Вронского:  . Следовательно,
. Следовательно,  и
и  составляют фундаментальную систему, и общее решение запишется
составляют фундаментальную систему, и общее решение запишется  . Составим теперь нормальную фундаментальную систему
. Составим теперь нормальную фундаментальную систему  , удовлетворяющую начальным условиям
, удовлетворяющую начальным условиям  . Очевидно,
. Очевидно,  представляются как линейные комбинации функций
представляются как линейные комбинации функций  и
и  :
:  . Для определения коэффициентов
. Для определения коэффициентов  пользуемся начальными условиями решений
пользуемся начальными условиями решений  :
:  . Отсюда
. Отсюда  ,
,  . При помощи функций
. При помощи функций  сразу запишем решение, удовлетворяющее условиям Коши: при
сразу запишем решение, удовлетворяющее условиям Коши: при 
 . Это решение будет
. Это решение будет  .
.
Мы видели, что формула (8) дает любое решение линейного однородного уравнения  -го порядка, если функции
-го порядка, если функции  линейно независимы. Отсюда получается доказательство такой теоремы.
линейно независимы. Отсюда получается доказательство такой теоремы.
Теорема 7. Если мы имеем  частных решений уравнения (3.1)
частных решений уравнения (3.1)  , то они являются линейно зависимыми.
, то они являются линейно зависимыми.
Для доказательства рассмотрим первые  функций:
функций:  . Возможны два случая:
. Возможны два случая:
1) Функции  линейно зависимы. Тогда теорема справедлива, так как линейное соотношение между
линейно зависимы. Тогда теорема справедлива, так как линейное соотношение между  функциями есть частный случай линейного соотношения между
функциями есть частный случай линейного соотношения между  функциями, где постоянный множитель при
функциями, где постоянный множитель при  равен нулю.
равен нулю.
2) Функции  линейно независимы. Тогда они образуют фундаментальную систему, через которую выражается линейным образом с постоянными коэффициентами любое частное решение. В частности, для
линейно независимы. Тогда они образуют фундаментальную систему, через которую выражается линейным образом с постоянными коэффициентами любое частное решение. В частности, для  получим
получим  . Это и есть искомая линейная зависимость. Теорема доказана.
. Это и есть искомая линейная зависимость. Теорема доказана.
Теорема 8. Если два линейных однородных уравнения
 (16)
(16)
имеют общую фундаментальную систему решений, то они тождественны между собой, т.е.  .
.
Докажем это. Вычитая почленно уравнения (16) получаем новое уравнение  -го порядка:
-го порядка:
 . (17)
. (17)
Если  и
и  не тождественно равны между собой, то найдется в силу их непрерывности интервал
не тождественно равны между собой, то найдется в силу их непрерывности интервал  , в котором
, в котором  . Разделив обе части уравнения (17) на
. Разделив обе части уравнения (17) на  , мы получим на интервале
, мы получим на интервале  уравнение вида (3.1), т.е. со старшим коэффициентом, равным 1. Очевидно по самому построению уравнения (17), что оно допускает те же решения, что и уравнения (16), т.е. уравнение
уравнение вида (3.1), т.е. со старшим коэффициентом, равным 1. Очевидно по самому построению уравнения (17), что оно допускает те же решения, что и уравнения (16), т.е. уравнение  -го порядка со старшим коэффициентом, равным 1, допускает (см. следствие теоремы 4)
-го порядка со старшим коэффициентом, равным 1, допускает (см. следствие теоремы 4)  независимых интегралов. Противоречие с теоремой 7 показывает, что
независимых интегралов. Противоречие с теоремой 7 показывает, что  . Таким образом, уравнение (17) имеет вид
. Таким образом, уравнение (17) имеет вид  . Рассуждение, подобно предыдущему, показывает, что
. Рассуждение, подобно предыдущему, показывает, что  , и далее таким же образом доказывается, что
, и далее таким же образом доказывается, что  .
.
Следствие. Фундаментальная система вполне определяет линейное однородное уравнение со старшим коэффициентом, равным 1.
Решим теперь такую задачу. Дана фундаментальная система на интервале  :
:  . Требуется построить соответствующее дифференциальное уравнение. Для этой цели приравниваем нулю следующий определитель, в котором
. Требуется построить соответствующее дифференциальное уравнение. Для этой цели приравниваем нулю следующий определитель, в котором  обозначает искомую функцию:
обозначает искомую функцию:
 . (18)
. (18)
Разлагая его по элементам последнего столбца, мы убеждаемся в том, что равенство (18) представляет собой однородное дифференциальное уравнение  -го порядка относительно функции
-го порядка относительно функции  . При подстановке вместо
. При подстановке вместо  функций
функций  , мы получаем определитель с двумя равными столбцами. Он тождественно равен нулю; следовательно, уравнение (18) допускает частные решения
, мы получаем определитель с двумя равными столбцами. Он тождественно равен нулю; следовательно, уравнение (18) допускает частные решения  .
.
Коэффициент при  есть
есть  . Он, как нам известно, не обращается в нуль на интервале
. Он, как нам известно, не обращается в нуль на интервале  . Разделив на него обе части уравнения (18), получим уравнение
. Разделив на него обе части уравнения (18), получим уравнение  -го порядка со старшим коэффициентом, равным единице, а по доказанному такое уравнение однозначно определяется фундаментальной системой. Задача, таким образом, решена.
-го порядка со старшим коэффициентом, равным единице, а по доказанному такое уравнение однозначно определяется фундаментальной системой. Задача, таким образом, решена.
Запишем уравнение (18) в развернутом виде:

Если исходное уравнение было записано в виде
 , (3.1)
, (3.1)
то сравнение коэффициентов дает нам тождество
 .
.
Легко убедиться в том, что определитель в числителе есть производная от определителя Вронского, стоящего в знаменателе. В самом деле, производная по 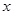 определителя, составленного из функций от
определителя, составленного из функций от 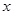 , равна сумме
, равна сумме  определителей, из которых у первого в первой строке функции заменены производными, а остальные не изменены; у второго во второй строке функции заменены производными, а остальные не изменены и т.д. У
определителей, из которых у первого в первой строке функции заменены производными, а остальные не изменены; у второго во второй строке функции заменены производными, а остальные не изменены и т.д. У  -го в последней строке функции заменены производными. Применяя это правило дифференцирования к определителю Вронского, мы получим
-го в последней строке функции заменены производными. Применяя это правило дифференцирования к определителю Вронского, мы получим  первых слагаемых в виде определителей, имеющих две равные строки, т.е. обращающиеся в нуль, а последнее слагаемое, не равное нулю, есть как раз числитель в выражении для
первых слагаемых в виде определителей, имеющих две равные строки, т.е. обращающиеся в нуль, а последнее слагаемое, не равное нулю, есть как раз числитель в выражении для  . Итак, мы имеем
. Итак, мы имеем  , откуда
, откуда  . Выражаем постоянную
. Выражаем постоянную  через начальное значение
через начальное значение  при
при  ; получаем окончательно
; получаем окончательно
 . (19)
. (19)
Равенство (19), определяющее определитель Вронского (с точностью до постоянного множителя) через коэффициент данного уравнения при  носит название формулы Остроградского-Лиувилля (Лиувилля).
носит название формулы Остроградского-Лиувилля (Лиувилля).
Применим формулу Остроградского-Лиувилля к нахождению общего решения уравнения второго порядка  , у которого нам известно одно частное решение
, у которого нам известно одно частное решение  . Пусть
. Пусть  есть любое решение этого уравнения, отличное от
есть любое решение этого уравнения, отличное от  . Составляем
. Составляем  и пишем его значение по формуле Остроградского-Лиувилля:
и пишем его значение по формуле Остроградского-Лиувилля:  . Получаем для
. Получаем для  линейное уравнение первого порядка. Раскрывая определитель, имеем
линейное уравнение первого порядка. Раскрывая определитель, имеем  . Деля обе части на
. Деля обе части на  , находим
, находим  , откуда
, откуда  определяется квадратурой
определяется квадратурой
 . (20)
. (20)
Полученное решение содержит две произвольные постоянные и, следовательно, является общим. Итак, если известно одно частное решение линейного однородного уравнения второго порядка, то общее решение находится квадратурами.
Пример 2. Легко убедиться в том, что уравнение  допускает частное решение
допускает частное решение  . В нашем случае
. В нашем случае  , и формула (20) дает
, и формула (20) дает

Это — общее решение данного уравнения.
Примечание 1. Всякое линейное дифференциальное уравнение (3.1) имеет бесконечное множество фундаментальных систем.
Примечание 2. Пусть  — любая система
— любая система  раз дифференцируемых линейно независимых функций. Если определитель Вронского не обращается в нуль на интервале
раз дифференцируемых линейно независимых функций. Если определитель Вронского не обращается в нуль на интервале  , то выражение (18) дает дифференциальное уравнение, имеющее данную систему в качестве фундаментальной.
, то выражение (18) дает дифференциальное уравнение, имеющее данную систему в качестве фундаментальной.
Примечание 3. Если составлять дифференциальное уравнение, допускающее в качестве фундаментальной системы наперед заданную систему из  линейно независимых функций, то точки, в которых определитель Вронского этой системы обращается в нуль, будут особыми точками построенного уравнения; в них будет обращаться в нуль коэффициент при
линейно независимых функций, то точки, в которых определитель Вронского этой системы обращается в нуль, будут особыми точками построенного уравнения; в них будет обращаться в нуль коэффициент при  .
.
Пример 3. Построить уравнение, имеющее в качестве фундаментальной системы функции  . Строим это уравнение по формуле (18):
. Строим это уравнение по формуле (18):  . Раскрывая определитель по элементам последнего столбца, получаем
. Раскрывая определитель по элементам последнего столбца, получаем  . Здесь
. Здесь  и не обращается в нуль на интервалах
и не обращается в нуль на интервалах  и
и  . Для этих интервалов имеем дифференциальное уравнение
. Для этих интервалов имеем дифференциальное уравнение  .
.
Зная одно нетривиальное частное решение  линейного однородного уравнения (3.1), можно подстановкой
линейного однородного уравнения (3.1), можно подстановкой  понизить порядок уравнения, сохранив его линейность и однородность.
понизить порядок уравнения, сохранив его линейность и однородность.
Действительно, подстановку  можно заменить двумя подстановками:
можно заменить двумя подстановками:
 (21)
(21)
и  . Линейное однородное преобразование (21) сохраняет линейность и однородность уравнения, следовательно, уравнение (3.1) преобразуется при этом к виду
. Линейное однородное преобразование (21) сохраняет линейность и однородность уравнения, следовательно, уравнение (3.1) преобразуется при этом к виду
 , (22)
, (22)
причем решению  уравнения (3.1) в силу (21) соответствует решение
уравнения (3.1) в силу (21) соответствует решение  уравнения (22). Подставляя
уравнения (22). Подставляя  в уравнение (22), получим
в уравнение (22), получим  . Следовательно, уравнение (22) имеет вид
. Следовательно, уравнение (22) имеет вид  , и подстановка
, и подстановка  понижает порядок на единицу:
понижает порядок на единицу:  . Заметим, что та же подстановка
. Заметим, что та же подстановка  , где
, где  — решение уравнения
— решение уравнения  , снижает на единицу и порядок линейного неоднородного уравнения
, снижает на единицу и порядок линейного неоднородного уравнения  , так как эта подстановка не затрагивает правой части уравнения.
, так как эта подстановка не затрагивает правой части уравнения.
Зная 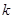 линейно независимых на отрезке
линейно независимых на отрезке  решений
решений  линейного однородного уравнения, можно понизить его порядок до
линейного однородного уравнения, можно понизить его порядок до  на том же отрезке
на том же отрезке  .
.
Действительно, понизив подстановкой  на единицу порядок уравнения (3.1), получаем опять линейное однородное уравнение
на единицу порядок уравнения (3.1), получаем опять линейное однородное уравнение
 (23)
(23)
порядка  , причем нам известны
, причем нам известны  его линейно независимых решений
его линейно независимых решений  которые получим, подставляя в
которые получим, подставляя в  или
или  последовательно
последовательно  . Заметим, что уже использованному нами для понижения порядка решению
. Заметим, что уже использованному нами для понижения порядка решению  уравнения (3.1) соответствует тривиальное решение
уравнения (3.1) соответствует тривиальное решение  уравнения (23).
уравнения (23).
Решения  линейно независимы, так как если бы между ними существовала линейная зависимость на отрезке
линейно независимы, так как если бы между ними существовала линейная зависимость на отрезке  :
:  или
или
 , (24)
, (24)
где хотя бы одно  , то, умножая на
, то, умножая на  и интегрируя тождество (24) в пределах от
и интегрируя тождество (24) в пределах от 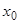 до
до 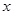 , где
, где  , а
, а 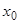 — точка отрезка
— точка отрезка  , будем иметь
, будем иметь
 ,
,
или, умножая на  и обозначая
и обозначая  , получим, вопреки исходному предположению, линейную зависимость между решениями
, получим, вопреки исходному предположению, линейную зависимость между решениями  :
:  , где хотя бы одно
, где хотя бы одно  . Итак, использовав одно частное решение
. Итак, использовав одно частное решение  , мы понизили порядок уравнения на единицу, сохранив его линейность и однородность, причем нам известно
, мы понизили порядок уравнения на единицу, сохранив его линейность и однородность, причем нам известно  линейно независимых решений преобразованного уравнения. Следовательно, тем же методом можно снизить порядок еще на одну единицу. Использовав еще одно решение и продолжая этот процесс
линейно независимых решений преобразованного уравнения. Следовательно, тем же методом можно снизить порядок еще на одну единицу. Использовав еще одно решение и продолжая этот процесс 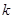 раз, получим линейное уравнение
раз, получим линейное уравнение  порядка.
порядка.
Пример 4.  . Это уравнение имеет очевидное частное решение
. Это уравнение имеет очевидное частное решение  . Понижая порядок подстановкой
. Понижая порядок подстановкой  ,
,  , приведем исходное уравнение к виду
, приведем исходное уравнение к виду  , откуда
, откуда  .
.