Принадлежность точки и линии поверхности

 

Рассмотрим построение проекций точки и линии последовательно на перечисленных выше поверхностях вращения.

 

Цилиндр

 

Пусть задан прямой цилиндр, плоскости основания которого параллельны плоскости П₁ (рис. 4.4).

Решим задачу. Зная фронтальные проекции точек А и В, лежащих на боковой поверхности цилиндра, построить отсутствующие проекции. Поскольку на П₁ боковая поверхность цилиндра проецируется в окружность, то А₁ и В₁ лежат, очевидно, на ней. Их положение находим по вертикальным линиям связи.

Профильные проекции А₃, В₃ лежат, как известно, на горизонтальных линиях связи с фронтальными проекциями А₂ и В₂. При этом, в соответствии с правилами ортогонального проецирования, расстояние от Ф₃ до профильной проекции точки равно расстоянию от Ф₁ до горизонтальной проекции точки. Причем точка В₃ – невидимая, так как лежит на невидимой части боковой поверхности цилиндра.

Решим следующую задачу: по заданной фронтальной проекции А₂В₂ линии (рис. 4.4) построим отсутствующие проекции.

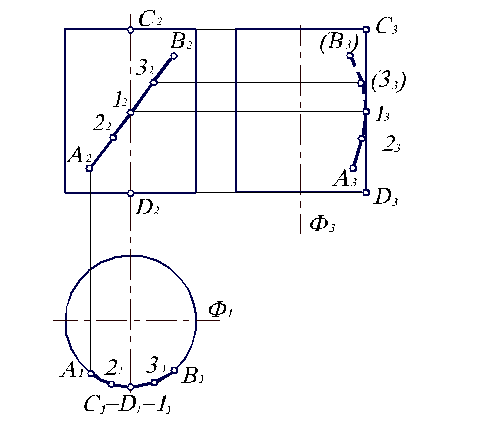
Горизонтальная проекция А₁В₁ совпадает с окружностью, так как все точки линии АВ лежат на боковой поверхности цилиндра.

При построении профильной проекции А₃В₃ следует иметь в виду, что линия АВ пересекает прямую СD, которая на П₃ является контуром С₃D₃ цилиндра. Поэтому сначала следует определить положение контурной точки 1₃, а затем соединить точки А₃ и В₃ линией, которая в отличии от А₂1₂В₂ не является прямой. В связи с этим для построения необходимо на А₂1₂В₂ выбрать несколько промежуточных точек (2₂, 3₂ и т.д.) и построить их профильные проекции (2₃, 3₃ и т.д.), руководствуясь вышеуказанным правилом взаимосвязи горизонтальной и профильной проекций. Чем большее количество промежуточных точек выбираем, тем более точными будут построения.

 

Конус

 

Решим те же задачи построения проекций точки и линии, лежащих на поверхности конуса (рис. 4.5).

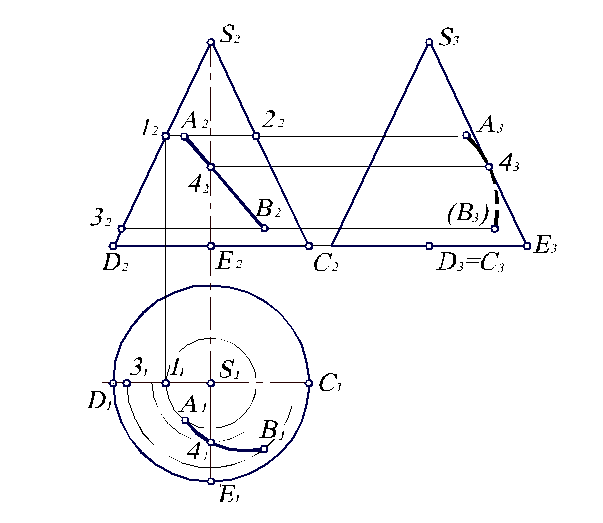
Рис. 4.5. Построение проекций точек и линии на поверхности конуса.

 

Построим отсутствующие проекции точек А и В, расположенных на поверхности прямого кругового конуса, если известно положение А₂ и В₂.

Для построение горизонтальной проекции точки, например А, необходимо через ее фронтальную проекцию провести горизонтальную линию. Тогда на П₁ эта линия 12 представляет собой дугу окружности диаметром 1₂2₂=1₁2₁. По линии связи на ней находим А₁. Аналогично, проводя дугу окружности радиусом S₁3₁, равным расстоянию от оси конуса до точки 3₂ на его контуре, определяем положение на ней точки В₁. По этим проекциям находим положение А₃, В₃.

По известной проекции А₂В₂ линии на поверхности конуса построить горизонтальную и профильную.

Выбрав на линии А₂В₂ промежуточную точку 4₂, найдем 4₁ так же, как сделали это для точек А и В. Соединив точки А₁, 4₁, В₁, получим горизонтальную проекцию линии АВ.

Для построения профильной проекции А₃В₃ необходимо найти положение контурной точки 4, лежащей на SA. По фронтальной проекции 4₂, лежащей на S₂A₂, находим профильную проекцию 4₃, лежащую на S₃A₃. Теперь точки А₃, 4₃, В₃ можно соединить линией.

При соединении точек линией всегда надо руководствоваться достаточно очевидным правилом: на каждой проекции точки, принадлежащие линии, следует соединять в одинаковой последовательности. Так, если на фронтальной проекции точка 4 является промежуточной, то она будет промежуточной и на других проекциях.

 

Сфера

 

Проекцией сферы на любую плоскость проекций является окружность.

Рассмотрим построение проекций точек на поверхности сферы (рис. 4.6). Задача состоит в том, чтобы по известным проекциям построить отсутствующие. Для упрощения решения необходимо все характерные точки сферы обозначить. Точки, лежащие на экваторе, обозначим через А, В, С, D; точки, лежащие на главном меридиане – А, Е, С, F. Очевидно, что точки А и С принадлежат одновременно и экватору, и главному меридиану.

Рис. 4.6. Построение проекций точек и линии на поверхности сферы.

 

При построении проекций следует иметь ввиду, что любая параллель на П₂ проецируется в горизонтальную прямую, а на П₁ в окружность.

Пусть задана фронтальная проекция точки М. Проведем через нее параллель. Тогда на П₂ получим горизонтальную прямую, проходящую через точку М₂. А на П₁ – дугу окрудности радиусом F₁1₁, равным расстоянию от вертикальной оси до токи 1₂. Ясно, что точка М₁ лежит на этой окружности. По двум проекциям М₁ и М₂, используя правило взаимосвязи проекций, построим М₃.

Рассмотрим другую точку N, проекция которой N₂ на П₂ является невидимой. Аналогично предыдущему построим N₁, лежащую на дуге окружности радиусом F₁2₁. Так как N₂ - невидимая, то N₁ лежит выше оси Ф₁. А поскольку точка N находится на поверхности нижнего полушария, что видно из положения N₂, то N₁ - невидимая. Профильная проекция N₃ строится по известному правилу взаимосвязи проекций. При этом, так как N₁ лежит выше оси Ф₁, то N₃ - левее Ф₃. Поскольку точка N лежит в правом полушарии, то на П₃ она невидимая, так как на П₃ все правое полушарие закрыто от нас левым и является невидимым.

Видимость и невидимость полушарий, а следовательно, и точек, лежащих на них, можно легко определить, рассматривая с разных точек зрения обыкновенный резиновый мячик, нарисовав на нем экватор и два меридиана, расположенных в плоскостях, перпендикулярных друг другу.

Построим горизонтальную и профильную проекции линии МN, если известна ее фронтальная проекция М₂N₂, состоящую из прямолинейных отрезков М₂3₂ и 3₂N₂.

Очевидно, что точка 3₁ лежит на А₁Е₁, так как 3₂ - на А₂Е₂. При этом прямая МN проходит через экватор (точка 4₂). Следовательно, на П₁ – через точку 4₁. А участок 4₁3₁ – невидимый, поскольку, как видно по его фронтальной проекции 4₂3₂, он лежит в нижнем полушарии, т.е. ниже экватора.

Для построения проекций участка 3N выберем промежуточную точку 5₂. Тогда точка 5₁ лежит на дуге окружности радиуса 5₂6₂. Соединив точки 3₁, 5₁, N₁, получим искомую линию М₁4₁3₁5₁N₁.

Построим профильную проекцию М₃N₃, которая проходит через те же промежуточные точки. Так как М₂3₂ – вертикальная прямая, то на П₃ она представляет собой дугу М₃3₃ окружности радиуса 4₂3₂=А₃3₃. Точка 5₃ – контурная для профильной проекции сферы. Значит, остается соединить точки 3₃, 5₃, N₃ кривой линией. При этом участок 5₃N₃ – невидимый.

Если в нашу задачу входит более точное построение проекций линии MN, тогда на всех участках, где ее проекции не являются отрезками прямой или окружности, необходимо выбрать несколько промежуточных точек.

Тор

 

Рассмотрим открытый тор, ось которого расположена вертикально, т.е. является горизонтально-проецирующей линией. Учитывая, что построение профильной проекции не вызывает больших затруднений, будем строить проекции лишь на П₁ и П₂ (рис. 4.7).

 

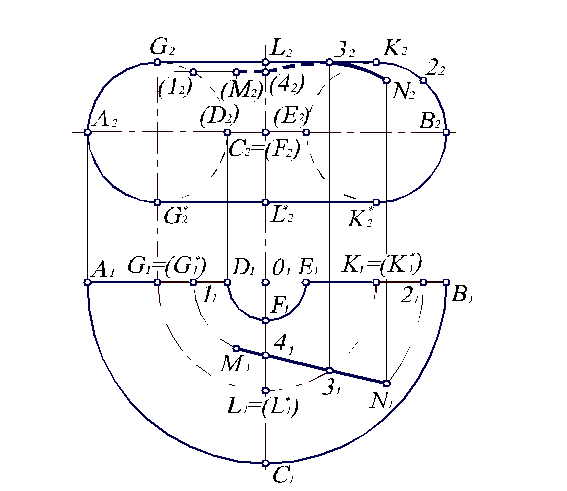
Рис. 4.7. Построение проекций точек и линии на поверхности тора.

 

Для удобства решения задач обозначим на рис. 4.7 характерные точки А, В, С, D, E, F, G, K, L, G*, K*, L*. Будем рассматривать переднюю половину поверхности тора.

По горизонтальным проекциям точек М и N построить фронтальные.

Для этого необходимо через точки М₁ и N₁ провести дуги окружности радиуса О₁М₁ и О₁N₁ соответственно до пересечения с прямой А₁В₁, где получим точки 1₁ и 2₁. По линиям связи построим точки 1₂ и 2₂, лежащие на окружностях, образующих поверхность тора. Через них проведем горизонтальные прямые, соответствующие дугам окружности на П₁. Следовательно, на них лежат точки М₂ и N₂. Так как контуром видимости является линия GLK, то точка M₂ – невидимая, а N₂ – видимая.

Построить фронтальную проекцию линии MN, горизонтальная проекция которой представляет собой прямую М₁N₁.

Точка 3₁, принадлежащая М₁N₁, лежит на контуре. Значит, ее положение на K₂L₂ можно получить по линии связи через 3₁. Очевидно, участок между точками N₂, 3₂ видимый, а между 3₂ и М₂ – невидимый. Так как невидимый участок достаточно протяженный, выберем некоторую промежуточную точку 4₁. Ее фронтальную проекцию 4₂ построим аналогично точкам M и N, проведя дугу окружности радиуса О₁4₁. Далее, соединив точки М₂, 4₂, 3₂, N₂, получаем окончательное решение. Кривая M₂N₂ состоит из невидимого М₂4₂3₂ и видимого 3₂N₂ участков.