Динамическое уравновешивание ротора

 

Рассмотрим динамически неуравновешенный ротор (рисунок 3.1). Можно было бы каждой неуравновешенной массе противопоставить свою корректирующую массу. Однако такое решение не является оптимальным, так как в системе ротора почти всегда происходит частичное взаимное уравновешивание.

Для уравновешивания двумя корректирующими массами, начало системы координат совмещаем с одной из плоскостей исправления, а ось Z направляем в сторону другой плоскости исправления.

Для устранения моментной неуравновешенности необходимо выполнение условия . В эту сумму входит и уравновешивающий момент дисбаланса, создаваемый корректирующей массой, которую размещаем во второй плоскости исправления. Величину этого момента можно определить графическим решением векторного уравнения.

 

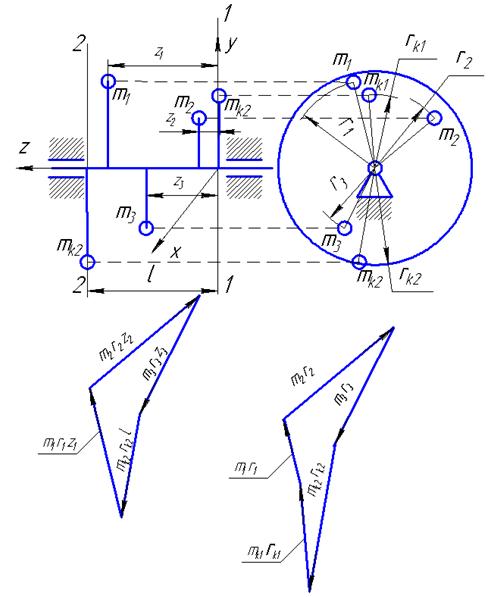
Рисунок 3.1

 

Для статического уравновешивания воспользуемся также векторным уравнением, только корректирующую массу будем добавлять в первую плоскость исправления, где координата Z =0 и первое условие уравновешивания не нарушится.

Графически решая это уравнение, находим уравновешивающий дисбаланс в первой плоскости исправления. Зная дисбалансы в плоскостях исправления, задаваясь одним из параметров (массой или радиусом, в зависимости от конструктивных соображений) определяем второй параметр.