ВРАЩЕНИЕ ТВЕРДОГО ТЕЛА ВОКРУГ НЕПОДВИЖНОЙ ТОЧКИ. ОБЩИЙ СЛУЧАЙ ДВИЖЕНИЯ ТЕЛА

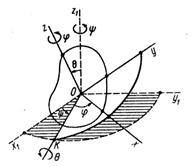Через неподвижную точку О твердого тела проведем неподвижную систему координат O₁x₁y₁ относительно которой будем рассматривать движение тела (рис. 39). Другую систему координат Oxyz скрепим с телом, вращающимся вокруг неподвижной точки О. Для определения положения движущегося тела относительно системы координат O₁x₁y₁ следует задать относительно этой системы координат положение другой, подвижной, системы координат Oxyz, скрепленной с движущимся телом. Для этой цели Эйлер предложил три независимых параметра – углы Эйлера.

Первый из этих углов – угол прецессии – определяет положение линии узлов ОК, которая является линией пересечения координатных плоскостей O₁x₁y₁ и Оху относительно неподвижной координатной оси Ox₁. Для изменения этого угла тело должно вращаться вокруг координатной оси Oz₁ которую называют осью прецессии.

Вторым углом Эйлера является угол между координатными плоскостями Ox₁y₁ и Оху. Его измеряют углом между перпендикулярами к этим координатным плоскостям, которыми являются оси Oz₁ и Oz.

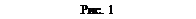Угол называют углом нутации, а ось ОК, вокруг которой вращается тело при изменении угла , соответственно называют осью нутации или линией узлов.

Для полного определения положения рассматриваемого тела относительно системы координат O₁x₁y₁z₁ нужно задать угол между подвижной осью координат Ох и положительным направлением линии узлов ОК – угол собственного вращения . Угол от линии узлов ОК до оси Ох считается положительным, если вокруг оси Oz поворот оси Ох от линии ОК виден происходящим против часовой стрелки.

При изменении угла тело вращается вокруг так называемой оси собственного вращения Oz, перпендикулярной плоскости, в которой лежат прямые ОК и Ох, образующие этот угол.

Углы Эйлера широко применяются в теории гироскопов.

В технике особенно важное значение имеет так называемая регулярная прецессия, когда угловые скорости вращения вокруг оси собственного вращения и вокруг неподвижной оси прецессии постоянны и угол между этими осями (угол нутации) остается тоже постоянным.

Итак, для определения положения тела с одной неподвижной точкой в любой момент времени надо задать углы Эйлера как однозначные функции времени, т. е.

; ; .

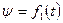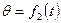Эти уравнения являются уравнениями вращения твердого тела вокруг неподвижной точки.