Потенциал Морзе

Для описания механической ангармоничности применяется множество модельных функций потенциальной энергии атомов в молекуле. Все они имеют сходство, обусловленное их физическим смыслом: резкое возрастание при стремлении R к нулю (соответствует отталкиванию ядер при сближении), минимум при , и возрастание до некоторого постоянного значения энергии диссоциации при R, стремящемся к бесконечности (ослабление взаимодействия и последующая диссоциация молекулы при больших расстояниях между атомами).

Одним из наиболее применяемых модельных потенциалов является потенциал Морзе [[2]]

где энергия диссоциации, отсчитываемая от минимума кривой потенциальной энергии и b подгоночный параметр, задающий ширину потенциальной ямы. На рис. 3 приведен график данной потенциальной функции (сплошная линия).

Разложение потенциала Морзе в ряд по переменной r около нуля начинается со слагаемого 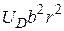. Это гармоническая составляющая потенциала Морзе (показана пунктирной линией на рис. 3). Ей соответствует гармоническая частота колебаний 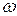, которую можно найти из соотношения

. (1.2)

На рис. 3 пунктирными горизонтальными отрезками показаны энергетические уровни гармонического осциллятора, а сплошными отрезками – уровни для потенциала Морзе. Видно, что по мере увеличения колебательной энергии энергетические уровни потенциала Морзе вследствие механической ангармоничности смещаются относительно уровней гармонического осциллятора. В отличие от гармонического осциллятора для потенциала Морзе разрешены переходы с

Важнейшим преимуществом потенциала Морзе перед другими является существование точного решения уравнения Шредингера [13]:

. (1.3)

Здесь 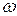− гармоническая частота колебаний, входящая в формулу 1.2.

Сопоставляя данное выражение с разложением 1.1, устанавливаем, что для потенциала Морзе параметры ангармоничности, начиная с y_e, равны нулю, а параметр связан с x_e и 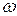соотношением . Параметр b также выражается через

r (отклонение от равновесного расстояния)

Рис. 3. Потенциал Морзе (сплошная линия) и его гармоническая составляющая (пунктир). Горизонтальными отрезками обозначены энергетические уровни данных потенциалов.

x_e и 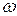: . Таким образом, определив из эксперимента параметры и 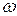, мы можем найти параметры потенциала Морзе b и .

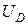Можно записать функцию потенциала Морзе в терминах x_e и :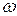

. (1.4)

Потенциал Морзе позволяет с хорошей точностью описать ход потенциальной кривой реальных молекул вблизи минимума (т.е. около точки r=0). Однако при (когда расстояние между ядрами равно нулю) вместо бесконечно большой потенциальной энергии потенциал Морзе дает конечное, хотя и очень большое значение.

В качестве примера, мы приведем параметры для свободного иона OH^‑ с =3738.44 см^-1 и =0.0244 [[3]] и для OD^‑ с =2721.3 см^-1 и =0.0176 [[4]]. Рассчитанные для OH^‑ и OD^‑ параметры потенциала Морзе оказались почти одинаковыми – наибольшая разница между ними меньше 0.5%. Этот результат легко объясняется. Действительно, рассматриваемые ионы отличаются друг от друга лишь массами ядер водорода H (состоящими из одного протона) и дейтерия D (протон + нейтрон). Электронные конфигурации данных ионов должны быть эквивалентны с очень большой точностью, так как нейтрон не имеет заряда, а гравитационное взаимодействие между нейтроном и электронами пренебрежимо мало. Следовательно, потенциальная функции взаимодействия ядер в ионе OH^‑ практически идентична потенциальной функции OD^‑.