I способ
Для того чтобы ответить на этот вопрос, сначала рассмотрим процесс  :
:
 ,
, ~
~  ,
,  .
.
Покажем, что этот ряд является стационарным процессом:
 ,
,
применим оператор  к
к 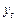 и так как
и так как  , тогда
, тогда
 ,
,
 (1).
(1).
По биному Ньютона
 ,
,
Тогда из уравнения (1) получим:
 .
.
Так как выполняется  , (
, ( ), то
), то
 (2),
(2),
где  — бесконечная убывающая геометрическая прогрессия
— бесконечная убывающая геометрическая прогрессия  .
.
Тогда применив формулу суммы бесконечной убывающей геометрической прогрессии получим:
 .
.
Теперь проверим, выполняются ли для данного ряда условия слабой стационарности:
 ,
,
так как  и
и  .
.
Применяя оператор  к
к 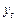 замечаем, что дисперсию суммы можно заменить на сумму дисперсий, так как все остатки независимы друг от друга.
замечаем, что дисперсию суммы можно заменить на сумму дисперсий, так как все остатки независимы друг от друга.
 ,
,
Используя свойство идентичности остатков, имеем:
 ,
,
если 
 =
=  < ∞. (Доказать в контрольной работе в задаче №9).
< ∞. (Доказать в контрольной работе в задаче №9).
Ряд  стационарен.
стационарен.
При  и
и  получаем
получаем  — стационарный ряд, «Белый шум»;
— стационарный ряд, «Белый шум»;
При  и
и  получаем
получаем  — «Случайное блуждание». Ряд не стационарен, так как из-за того, что
— «Случайное блуждание». Ряд не стационарен, так как из-за того, что 
 и
и  .
.
Как еще отличить  от случайного блуждания? В записи (2) видно, что влияние возмущений со временем уменьшается (при
от случайного блуждания? В записи (2) видно, что влияние возмущений со временем уменьшается (при  ), то есть возмущение в момент времени
), то есть возмущение в момент времени  меньше чем в момент
меньше чем в момент  и так далее. При
и так далее. При  влияние возмущения со временем не затухает, то есть возмущения в момент времени
влияние возмущения со временем не затухает, то есть возмущения в момент времени  ,
,  вносят такой же вклад как и et в момент времени
вносят такой же вклад как и et в момент времени  .
.