Более компактная (универсальная) запись различных моделей
Для того чтобы сделать модель более компактной используют оператор сдвига (lag operator).
Обозначение оператора сдвига — 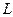 .
.
Запись 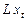 означает сдвиг
означает сдвиг  на один период назад:
на один период назад:
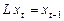 .
.
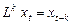 — эта запись означает применение оператора сдвига к объясняющей переменной
— эта запись означает применение оператора сдвига к объясняющей переменной 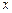 в момент времени
в момент времени 
 раз, то есть переменная
раз, то есть переменная 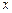 от момента времени
от момента времени  сдвигается влево (назад) на
сдвигается влево (назад) на  лагов.
лагов.
Пример:
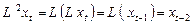 .
.
Введем обозначение полиномов оператора сдвига:
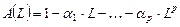 , где
, где 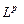 означает, что оператор
означает, что оператор 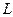 применен
применен 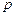 раз;
раз;
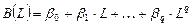 — для DL моделей;
— для DL моделей;
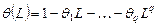 , где
, где 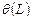 — оператор, применяемый к остаткам;
— оператор, применяемый к остаткам;
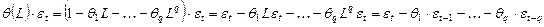 .
.
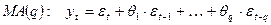 — запись «Moving Average» (скользящая средняя).
— запись «Moving Average» (скользящая средняя).
Упражнение. Получить полином оператора сдвига 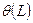 для следующей спецификации MA(q):
для следующей спецификации MA(q):
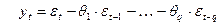 .
.
Имеет ли значение знак перед коэффициентом 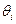 в спецификации MA(q) и почему?
в спецификации MA(q) и почему?
В общем виде, с использованием операторов полиномов, любая модель временных рядов может быть записана следующим образом:
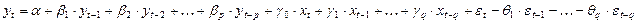 ,
,
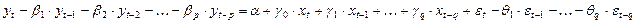 ,
,
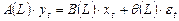 .
.
Если в спецификации модели (конкретной формуле) присутствует только запись 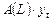 , то это означает, что модели относятся к классу AR.
, то это означает, что модели относятся к классу AR.
Если в спецификации модели (конкретной формуле) присутствует только запись 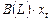 , то это означает, что модели относятся к классу DL.
, то это означает, что модели относятся к классу DL.
Если в спецификации модели (конкретной формуле) присутствует только запись 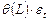 , то это означает, что модели относятся к классу MA.
, то это означает, что модели относятся к классу MA.
Задача:
Используя регрессионный аппарат построить зависимость для прогнозирования объема реализации на основе данных о динамике этого показателя (данные в условных единицах):
17, 16, 21, 24, 23, 26, 28.
Дано уравнение регрессии вида
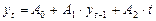 .
.
В данном примере построена модель временного ряда с использованием зависимости от времени (t).
Для нахождения коэффициентов регрессии поставим задачу МНК:
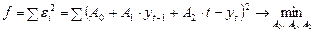 ,
,
Необходимые условия экстремума:
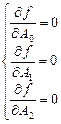 ,
,
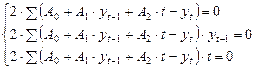 ,
,
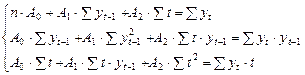 .
.
Построим таблицу и рассчитаем в ней все необходимые коэффициенты.

| 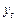
| 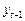
| 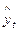
| 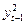
| 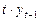
| 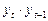
| 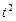
| 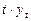
|
| 17,43662 | ||||||||
| 2,10387 | ||||||||
| -0,36444 | ||||||||
| 0,00000 | ||||||||
| 0,00000 | ||||||||
| 0,00000 | ||||||||
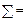 21 21
| 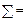 138 138
| 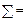 127 127
| 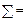 19,176 19,176
| 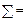 2767 2767
| 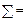 479 479
| 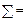 2990 2990
| 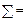 91 91
| 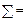 520 520
|
Получим систему уравнений:
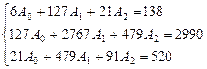 .
.
Решим данную систему методом Гаусса и получим значения искомых коэффициентов для уравнения регрессии:
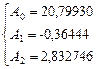 .
.
Таким образом, уравнение регрессии примет вид:
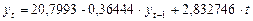 .
.
Результат можно проверить, построив модель в пакете Statistica 6.0.
Для проверки качества модели рассчитывается следующий коэффициент:
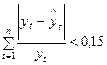
Если его значение меньше 15%, то уравнение можно использовать в целях прогнозирования.