Статистические методы принятия решений в условиях риска

 

Количественная оценка предпринимательского риска вне за­висимости от содержания конкретной задачи возможна, как пра­вило, с помощью методов математической статистки. Главные инструменты данного метода оценки — дисперсия, стандартное отклонение, коэффициент вариации.

Для оценки величины риска (степени риска) остановимся на следующих критериях:

1) среднее ожидаемое значение;

2) колеблемость (изменчивость) возможного результата.

Для статистической выборки

xi x1 x2 … xi
ni n1 n2 … ni

где xi — ожидаемое значение для каждою случая наблюдения (i = 1,2,...),

ni — число случаев наблюдения (частота) значения хi,

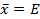— среднее ожидаемое значение,

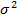дисперсия,

V — коэффициент вариации,

имеем:

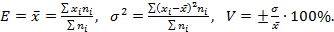(3.5)

 

Рассмотрим задачу об оценке риска по хозяйственным кон­трактам. ООО «Интерпродукт» решает заключить договор на поставку продуктов питания с одной из трех баз. Собрав данные о сроках оплаты товара этими базами (табл. 3.3), нужно, оценив риск, выбрать ту базу, которая оплачивает товар в наименьшие сроки при заключении договора поставки продукции.

Таблица 3.3

Номер события Сроки оплаты в днях Число случаев наблю­дения п хn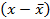
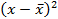
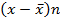
1-я база
-5,61 31,47 944,10
-1,61 2,59 72,58
-0,61 0,37 8,19
2,39 5,71 228,40
4,39 19,27 578,10
Σ       1831,37
2-я база
-6,61 43,69 1267,07
-2,61 6,81 143,05
-1,61 2,59 93,16
0,39 0,15 7,5
2,39 5,71 177,07
6,39 40,83 1347,46
Σ       3035,31
3-я база
-8,58 73,62 3091,89
-6,58 43,30 1472,20
-0,58 0,34 10,76
0,42 0,18 4,94
2,42 5,86 199,12
5,42 29,38 851,92
6,42 41,22 1071,63
7,42 55,06 1376,41
Σ       8078,87

 

Для первой базы, исходя из формул (3.5):

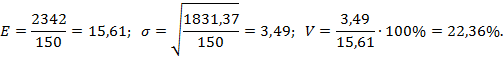
Для второй базы

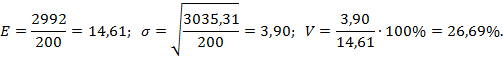
Для третьей базы

 

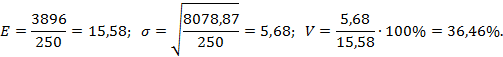
Коэффициент вариации для первой базы наименьший, что го­ворит о целесообразности заключить договор поставки продук­ции с этой базой.

Рассмотренные примеры показывают, что риск имеет матема­тически выраженную вероятность наступления потери, которая опирается на статистические данные и может быть рассчитана с достаточно высокой степенью точности. При выборе наиболее приемлемого решения было использовано правило оптимальной вероятности результата, которое состоит в том, что из возмож­ных решений выбирается то, при котором вероятность результа­та является приемлемой для предпринимателя.

На практике применение правила оптимальной вероятности результата обычно сочетается с правилом оптимальной колебле­мости результата.

Как известно, колеблемость показателей выражается их дис­персией, средним квадратическим отклонением и коэффициентом вариации. Сущность правила оптимальной колеблемости резуль­тата заключается в том, что из возможных решений выбирается то, при котором вероятности выигрыша и проигрыша для одного и того же рискового вложения капитала имеют небольшой раз­рыв, т.е. наименьшую величину дисперсии, среднего квадратичес-кого отклонения вариации. В рассматриваемой задаче выбор оптимального решения был сделан с использованием этих двух правил.