Вероятностная постановка принятия предпочтительных решений
Риск — категория вероятностная, поэтому в процессе оценки неопределенности и количественного определения риска используют вероятностные расчеты.
Вероятностные задачи характеризуются тем, что эффективность принимаемых решений зависит не только от детерминированных факторов, но и от вероятностей их появления, т.е. известен закон распределения управляемых факторов X в виде:
| x | x1 | x2 | … | xn |
| P | P1 | P2 | … | Pn |
где Pi есть вероятность появления управляемого фактора хi, i = 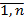 .
.
Каждой паре (хi, Рi) соответствует значение функции эффективности E(xi, Pi). В качестве показателей эффективности могут выступать математическое ожидание Е, дисперсия D, среднее квадратическое отклонение и другие вероятностные характеристики.
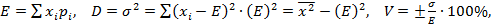 (3.1)
(3.1)
где Е2 — среднее ожидаемое значение квадрата рассматриваемой величины.
Средняя величина Е представляет собой обобщенную количественную характеристику и не позволяет принять решение в пользу какого-либо варианта вложения капитала.
Среднее квадратическое отклонение σ является именованной величиной и указывается в тех же единицах, в каких измеряется варьирующий признак. Дисперсия и среднее квадратическое отклонение являются мерами абсолютной колеблемости.
Дисперсия не дает полной картины линейных уклонений ΔХ = Х - Е, более наглядных для оценивания рисков. Тем не менее, задание дисперсии позволяет установить связь между линейным и квадратичными отклонениями с помощью известного неравенства Чебышева.
Вероятность Р того, что случайная величина X отклоняется от своего математического ожидания больше, чем на заданный допуск ε > 0, не превосходит ее дисперсии, деленной на ε2, т.е.
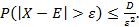 (3.2)
(3.2)
Отсюда видно, что незначительному риску по среднеквадратическому отклонению соответствует малый риск и по линейным отклонениям: точки X с большой вероятностью будут располагаться внутри ε — окрестности ожидаемого значения Е.
Все более признанным становится оценка рискованности посредством среднего квадратического отклонения σ.
Итак, будем считать, что риском операции называется число σ — среднее квадратическое отклонение управляемого фактора (например, дохода) X операции, которое обозначим r = σ.
Если, например, под X понимать случайный доход Q, то EQ представляет собой средний ожидаемый доход, или эффективность, а среднее квадратическое отклонение σQ является оценкой рискованности, риском и обозначается rQ.
Коэффициент вариации V — безразмерная величина. С его помощью можно сравнивать даже колеблемость признаков, выраженных в разных единицах измерения. Коэффициент вариации изменяется от 0 до 100%. Чем больше коэффициент, тем сильнее колеблемость. Установлена следующая качественная оценка различных значений коэффициента вариации: до 10% — слабая колеблемость, 10—25% — умеренная колеблемость, свыше 25% — высокая колеблемость.
С помощью этого метода оценки риска, т.е. на основе расчета дисперсии, стандартного отклонения и коэффициента вариации можно оценить риск не только конкретной сделки, но и предпринимательской фирмы в целом (проанализировав динамику ее доходов) за некоторый промежуток времени.
Преимуществом данного метода оценки предпринимательского риска является несложность математических расчетов, а явным недостатком — необходимость большого числа исходных данных (чем больше массив, тем достовернее оценка риска).
Рассмотрим данный метод на конкретном примере. Сравним по риску вложения в акции трех типов А, В, С, если каждая из них по своему откликается на возможные рыночные ситуации, достигая с известными вероятностями определенных значений доходности (табл. 3.1).
Таблица 3.1
| Тип акций | Ситуация 1 | Ситуация 2 | ||
| вероятность | доходность | вероятность | доходность | |
| А | 0,5 | 20% | 0,5 | 10% |
| В | 0,99 | 15,1% | 0,01 | 5,1% |
| С | 0,7 | 13% | 0,3 | 7% |
По формулам (3.1) находим для акции А:
ЕА = 20 • 0,5 + 10 • 0,5 = 15%,
DA = (20 - 15)2 • 0,5 + (10 - 15)2 • 0,5 = 25,
σA =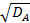 =5%,
=5%, 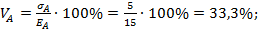
для акции В:
ЕB = 15,1 • 0,99 + 5,1 • 0,01 = 15%,
DB = (15,1 - 15)2 • 0,99 + (5,1 - 15)2 • 0,01 = 0,99,
σB = 0,995%, 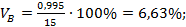
для акции С:
ЕC = 13 • 0,7 + 7 • 0,3 = 11,2%,
DC = (13 – 11,2)2 • 0,7 + (7 – 11,2)2 • 0,3 = 7,56,
σC = 2,75%, 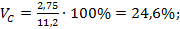
Так как наименьшее значение коэффициента вариации имеем для акции В, то и вложения в эту акцию наиболее предпочтительны, тем более, что и σB = rB = 0,995% наименьшее.
Особый вариант риска связан с разорением. Так называется вероятность столь больших потерь (х < Е), которые ЛПР не может компенсировать и которые, следовательно, ведут к его разорению.
Пример. Пусть случайный доход операции О имеет следующий ряд распределения:
| O: | -60 | -40 | -30 | |
| 0,1 | 0,2 | 0,5 | 0,2 |
и потери 30 или более ведут к разорению ЛПР. Следовательно, вероятность возникновения риска разорения в результате данной операции равна 0,1 + 0,2 + 0,5 = 0,8.
Серьезность риска разорения оценивается именно величиной соответствующей вероятности. Если эта вероятность очень мала, то ею часто пренебрегают (в конце концов вероятность разорения отлична от нуля почти в любой сделке — из-за весьма маловероятных катастрофических событий на финансовых рынках, в масштабах государства, из-за природных явлений и т.п.).
Определим вероятностную меру разорения, приписывая ей вероятность осуществления подобного события.
Пример. Предположим, что на рынке могут возникнуть только два исхода и на каждый из них акции А и В откликаются неслучайным образом. Вероятности этих исходов и соответствующих им значений доходности задаются табл. 3.2.
Таблица 3.2
| Исход 1 | Исход 2 | |||
| вероятность | доходность | вероятность | доходность | |
| А | 0,3 | 6% | 0,7 | 2% |
| В | 0,2 | -1% | 0,8 | 4,25% |
Ожидаемые доходности акций:
ЕА = 6 • 0,3 + 2 • 0,7 = 3,2%, ЕB = - 1 • 0,2 + 4,25 • 0,8 = 3,2%
совпадают, а дисперсии (квадратичные характеристики рисков) равны:
DA = (6 - 3,2)2 • 0,3 + (2 - 3,2)2 • 0,7 = 3,35, σА = rА = 1,83,
DB = (- 1 - 3,2)2 • 0,2 + (4,25 - 3,2)2 • 0,8 = 3,41, σB = σB = 1,85.
Предположим теперь, что инвестор взял деньги в долг под процент, равный 2,5%. Ставка процента по кредиту ниже ожидаемой доходности по акциям, которые будут приобретены на заемные деньги, поэтому действия инвестора вполне разумны.
Однако, если инвестор вложил деньги в акции А, то при исходе 1 он выиграет (6 - 2,5) = 3,5%, а при исходе 2 проиграет (2 - 2,5) = - 0,5%, причем с вероятностью Р2 = 0,7. Напротив, если он вложит деньги в актив В, то разорение ему грозит с вероятностью Р1 = 0,2 в первой ситуации (исход 1), когда он теряет (- 1 - 2,5) = - 3,5%.
Подсчитаем ожидаемые потери (П) при покупке акций А и В соответственно: ПА = 0,5 • 0,7 = 0,35, ПВ = 3,5 • 0,2 = 0,7.
Как видим, в первом случае они меньше. Зато риски разорения, оцениваемые через вероятность наступления события, наоборот, при приобретении акций А будут больше (0,7 > 0,2). Это превышение возможности банкротства должно отпугивать осторожного вкладчика, который к тому же «играет» на заемном капитале, от акции А в пользу бумаг В.
В свою очередь, ожидаемый риск ПА < ПВ склоняет его к выбору в пользу акций А. Как действовать в подобной ситуации инвестору? Это зависит от его индивидуальных предпочтений, выражаемых в том числе, функцией полезности инвестора.
В рассматриваемых статистических играх используются понятия: риск (функция риск), потери (функция потерь), решение (функция решения), функции распределения при определенных условиях.
Между определенностью и неопределенностью находится случай принятия решения в условиях риска, когда можно оценить вероятность возникновения каждого возможного условия. Широко используемый подход при таких обстоятельствах — критерий предполагаемого выигрыша.
Предполагаемый выигрыш рассчитывается для каждой альтернативы, после чего отбирается альтернатива с самым высоким показателем. Предполагаемый выигрыш — это сумма значений выигрыша для каждой альтернативы, причем, каждое значение взвешивается с точки зрения вероятности соответствующего условия. Таким образом, используя критерий предполагаемого выигрыша, можно определить возможное значение выигрыша для каждой альтернативы и выбирать вариант с наилучшим значением выигрыша.
В случае стохастической неопределенности, когда неуправляемым факторам (состояниям природы) поставлены в соответствие вероятности, заданные экспертно или вычисленные, решение обычно принимается на основе критерия максимума ожидаемого среднего выигрыша или минимума ожидаемого среднего риска.
Если для каждой игры с природой, задаваемой платежной матрицей Р = 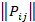 , i =
, i = 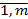 , j =
, j = 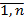 , стратегиям природы Пj, соответствуют вероятности Pj, то лучшей стратегией игрока один будет та, которая обеспечивает ему максимальный средний выигрыш, т.е.
, стратегиям природы Пj, соответствуют вероятности Pj, то лучшей стратегией игрока один будет та, которая обеспечивает ему максимальный средний выигрыш, т.е.
 (3.3)
(3.3)
Применительно к матрице рисков (матрице упущенных возможностей (выгод)) лучшей будет та стратегия игрока, которая обеспечивает ему минимальный средний риск
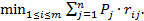 (3.4)
(3.4)
Когда говорится о среднем выигрыше или риске, то подразумевается многократное повторение процесса принятия решений, хотя реально требуемого количества повторений чаще всего может и не быть.
Пусть платежная матрица имеет вид:
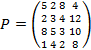
По формуле
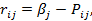
где 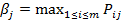 при заданном j, строим матрицу рисков R.
при заданном j, строим матрицу рисков R.
Находим β1 = max (5, 2, 8, 1) = 8, β2 = 5, β3 = 8, β4 = 12 и тогда

Предположим, что вероятности Рj равны: Рj = 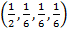 . По формуле (3.4) находим средний ожидаемый риск:
. По формуле (3.4) находим средний ожидаемый риск:
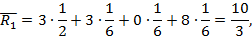
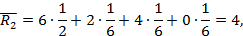
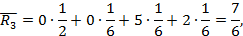
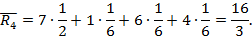
Минимальный средний ожидаемый риск: 
По формуле (3.3) найден средний ожидаемый выигрыш
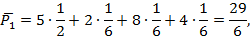
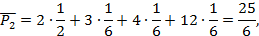
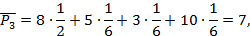
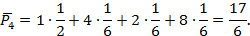
Максимальный средний ожидаемый доход 
Вероятностная постановка задачи выбора оптимальных решений в экономике более адекватно отображает реальные ситуации. Поэтому применение вероятностных моделей во многих случаях позволяет уменьшить риск при выборе наиболее эффективных решений. Однако применение указанных моделей связано с необходимостью определения вероятностных характеристик анализируемых процессов (ситуаций). Это существенно усложняет решение рассматриваемых задач. Во многих случаях вероятностное распределение экономических показателей бывает неизвестным. Поэтому возникает необходимость определения предпочтительных альтернатив при условии, что вероятностные характеристики экономических показателей являются неизвестными.
В условиях полной неопределенности, когда вероятности рассматриваемых ситуаций неизвестны, можно пользоваться правилом Лапласа, заключающимся в том, что все неизвестные вероятности Pj считают равными. После этого выбор эффективного решения можно принимать или по правилу максимизации среднего ожидаемого выигрыша или по правилу минимизации среднего риска. Подобный критерий принятия решения можно назвать принципом недостаточного обоснования Лапласа.