Закон Ома. Сопротивление проводников.

Немецкий физик Г.Ом (1787-1854) экспериментально установил, что сила тока , текущая по однородному металлическому проводнику ( то есть проводнику в котором не действуют сторонние силы), пропорциональна напряжению на концах проводника

, (1)

- электрическое сопротивление проводника.

1). Закон Ома для однородного участка цепи.

 

	Цепь не содержит эдс. В этом случае напряжение совпадает с разностью потенциалов и (1)
Рис.3.

 

2). Закон Ома для неоднородного участка цепи.

 

	Цепь содержит эдс. В этом случае
Рис. 4.

 

3). Закон Ома для замкнутой цепи.

 

	В этом случае и поэтому . Формула (1) позволяет установить единицу сопротивления Ом (Ом). 1Ом – сопротивление такого проводника, в котором при напряжении 1В течет постоянный ток 1А.
Рис.5.

 

Величина

называется электрической проводимостью проводника. Единица проводимости – сименс (См). 1См – проводимость участка электрической цепи сопротивлением 1Ом.

Сопротивление проводников зависит от его размеров и формы, а также от материала, из которого проводник изготовлен. Для цилиндрического проводника сопротивление прямо пропорционально его длине и обратно пропорционально площади его поперечного сечения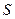

, (2)

где -коэффициент пропорциональности, характеризующий материал проводника. Он называется удельным электрическим сопротивлением. Единица удельного электрического сопротивления Ом м. Наименьшим удельным сопротивлением обладают серебро (1,6 10 ^-8 Ом м) и медь (1,7 10^-8 Ом м). На практике наряду с медными применяются алюминиевые провода, хотя алюминий и имеет большее, чем медь, удельное сопротивление (2,6 10 ^-8 Ом м), но зато обладает меньшей плотностью по с равнению с медью

Закон Ома можно представить в дифференциальной форме. Подставив выражение для сопротивления (2) в закон Ома (1) получим

, (3)

где величина

,

обратная удельному сопротивлению, называется удельной проводимостью вещества проводника. Ее единица – См/м (сименс на метр). Учитывая, что - напряженность электрического поля в проводнике, - плотность тока, формулу (3) можно переписать в виде

. (4)

Так как носители заряда в каждой точке движутся в направлении вектора напряженности то направления и совпадают, и (4) можно записать в виде

. (5)

Выражение (5) – закон Ома в дифференциальной форме, связывающий плотность тока в любой точке внутри проводника с напряженностью электрического поля в этой же точке. Это соотношение справедливо и для переменных полей.

При последовательном соединении проводников их сопротивления складываются,

,

а при параллельном соединении – суммируются обратные значения сопротивлений,

.

Опыт показывает, что в первом приближении изменение удельного сопротивления, а следовательно, и сопротивление с температурой описывается линейным законом

,

,

где и - соответственно удельные сопротивления и сопротивления проводника при и 0 ⁰С, - температурный коэффициент сопротивления, для чистых металлов ( при не очень низких температурах) близкий к 1/273 град -1. Поэтому температурная зависимость сопротивления металла может быть представлена в виде

,

где - термодинамическая температура.

Качественная температурная зависимость сопротивления металла представлена на рис. 6 (кривая 1).

В последствии было обнаружено, что сопротивление многих металлов ( например, Al, Pb, Zn и др.) и их сплавов при очень низких температурах = 0,14 – 20 К, называемых

	критическими, характерных для каждого вещества, скачкообразно уменьшается до нуля (кривая 2), то есть металл становится абсолютным проводником. Впервые это явление, называемое сверхпроводимостью, обнаружено Г. Камерлинг – Оннесом для ртути.
Рис. 6.

Явление сверхпроводимости объясняется на основе квантовой теории. Практическое использование сверхпроводящих материалов затруднено из-за низких температур. Поэтому в настоящее время ведется интенсивный поиск высокотемпературных сверхпроводящих соединений.

На зависимости электрического сопротивления металлов от температуры основано действие термометров сопротивления, которые позволяют измерять температуру с точностью до 0,003 К. Использование же в качестве рабочего вещества термометров сопротивления полупроводников, приготовленных по специальной технологии – термисторов – позволяет отмечать изменение температуры в миллионные доли кельвина и использовать термисторы для измерения температур очень малых объемов (ввиду малых габаритов полупроводников).