Поляризация.

Поляризация P (сумма дипольных моментов в единице объема)

P=N_общ, где:

-оператор дипольного момента

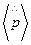- средняя величина квантово-механическая

- средняя величина по ансамблю

N_общ – число частиц в единице объема

=

-гамильтониан, оператор полной энергии.

, - может быть 2 состояния, и .

В общем случае , где -без взаимодействия, -дипольное взаимодействие.

,

Энергия взаимодействия : ,

Гамильтониан всей системы: =

Уравнение для каждого матричного элемента матрицы плотности:

,

N₁=N_общ, N₂=N_общ, ,

Если посмотреть на уравнения 1 и 2, то при поле =0 населенности должны остаться теми же, как и во время генерации.

«От руки» мы должны дописать слагаемое – релаксационные члены (в отсутствии поля генерации)

где Т1 –время продольной релаксации, Т2 –время поперечной релаксации.

Уравнения учитывают релаксационные члены.

Надо получить уравнение для поляризации и инверсии населенностей.