Тема: Устойчивость линейных систем.
Устойчивость представляет собой способность САР возвращается к исходному состоянию после кратковременного внешнего воздействия. Необходимым и достаточным условием устойчивости линейной САР является отрицательность вещественных частей всех корней ее характеристического уравнения. Попытка анализа устойчивости линейных САР путем прямого отыскания корней характеристического уравнения наталкивается на практические трудности связанные с отсутствием аналитических выражений для корней уравнения степени выше 4-ой. Однако нет необходимости находить значения корней, поскольку для суждения об устойчивости системы, нужно знать только то, что все они расположены левее мнимой оси на плоскости комплексного переменного S.
ТАУ пользуется условиями, которые позволяют судить о расположении корней в левой полуплоскости без нахождения их значений. Эти условия называются критериями устойчивости.
Существуют2 группы критериев: алгебраические и частотные.
Алгебраические:
1. критерий Гурвица.
Дано характеристическое уравнение системы 
необходимо составить определитель Гурвица из коэффициентов уравнения.
Правило составления определителя: по правой диагонали записывается n-е количество коэффициентов, начиная со 2-го (an-1). Сверху от элементов главной диагонали в каждом столбце записываются коэффициенты с последовательно убывающими индексами, а снизу с возрастающими индексами. При этом на место коэффициентов с индексами большими n или меньшими нуля записываются нули. Получается определитель, содержащий n-строк и n-столбцов. Далее составляются главные диагональные миноры определителя Гурвица.
Критерий устойчивости Гурвица формируется следующим образом, для устойчивости линейных САР с характеристическим уравнением вида , необходимо и достаточно, чтобы при an>0, все главные диагональные миноры определителя Гурвица были положительны. Частный случай условия устойчивости для уравнения 1-ой и 2-ой степеней сводится к требованию положительности коэффициентов характеристического уравнения.
2. критерий Рауса.
Составляем таблицу Рауса:
| - | c11=an | c21=an-2 | … |
| - | c12=an-1 | c22=an-3 | … |
| r=c11/c12 | c13=c21-r3c22 | c23=c31-r3c32 | … |
| r=c12/c13 | c14=c22-r4c23 | c24=c32-r4c33 | … |
| r=c13/c14 | c15=c23-r5c24 | c25=c33-r5c34 | … |
Правило составления таблицы:
любой из коэффициентов таблицы Рауса можно найти по формуле 
, где 
.
Определение критерия Рауса: для устойчивости САР необходимо и достаточно, чтобы коэффициенты 1-го столбца таблицы Рауса были положительными.
Частотные:
- критерий Михайлова.
Дано характеристическое уравнение вида
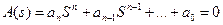
Для устойчивости САР необходимо и достаточно, чтобы годограф A(jω), начиная с ω=0 на действительной оси с ростом ω от 0 до ∞ обходят последовательно в положительном направлении (против часовой стрелки) n квадрантов, где n – порядок характеристического уравнения.
На рисунке показаны годографы Михайлова для устойчивых систем, при различных значениях n. Все они меняются при ω=0 на положительной действительной полуоси. Годографы уходят в бесконечность, при ω→∞ и обходят соответствующие число квадрантов в положительном направлении.
На этом рисунке показаны годографы неустойчивых систем, все они не удовлетворяют условию обхода n – квадрантов положительного направления.
- критерий Найквиста.
Рассмотрим 3 случая состояния разомкнутой системы: устойчива, неустойчива и находится на границе устойчивости.
1 случай (система устойчива). Для устойчивости замкнутой САР необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы φр(jω) при изменении ω от 0 до ∞ не охватывает точку (-1, j0).
2 случай (система неустойчива). Для устойчивости замкнутой САР необходимо и достаточно, чтобы частотный годограф комплексного коэффициента передачи разомкнутой системы φр(jω) при изменении ω от 0 до ∞ охватывал L/2 рода в положительном направлении точку (-1,j0), где L – число корней характеристического уравнения разомкнутой системы в правой полуплоскости.
3 случай (система на гране устойчивости). В этом случае нельзя пользоваться приведенными выше формулировками критерия Найквиста. Путем искусственного сдвига нулевых корней Si=±β, с последующим предельным переходом β→0 рассматриваемый случай можно свести к случаю устойчивости или неустойчивости системы, что дает возможность применить приведенные выше формулировки критерия Найквиста.
Система называется структурно не устойчивой, если ни каким изменениям коэффициентов нельзя достичь устойчивости.
Система называется структурно устойчивой, если устойчивости можно достичь изменением коэффициентов.
Для стабилизации структурно не устойчивых систем их структуру надо изменить таким образом, чтобы уменьшить степень передаточных функций, а это достигается введением внутренней обратной связи, охватывающей один из интеграторов, либо введением дифференцирующего звена.
Степень передаточной функции равна разности степеней знаменателя и числителя.