Теорема

Можно показать, что необходимым и достаточным условием разрешимости проблемы размещения собственных чисел системы с регулятором путем выбора матрицы является не вырожденность пары матриц , что означает . Если условие управляемости не выполняется, то выбор матрицы не влияет на значение процессов 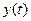и , и это означает, что система не может быть стабилизирована.



‚

– вектор состояния в новом базисе;

– вектор состояния в старом базисе;

 

, где

– матрица перехода от старого базиса к новому базису

 

Представим систему в новом базисе:

;
;

; – уравнение динамики в новом базисе

;

 

; – матрица динамики в новом базисе

;

. – матрица выхода в новом базисе

 

Пусть система  является управляемой, опишем систему охваченной ОС в новом базисе:

;

;

;

При ,

.

 

.

 

Матрица должна быть выбрана таким образом, чтобы матрица динамики в новом базисе была бы в форме Калмана, при этом матрица входа в новом базисе при была бы единичным вектором столбцом.

 

Матрица динамики в форме Калмана может быть записана:

, где

– коэффициенты характеристического уравнения .

.

 

в этом случае будет просто столбец, т.е. .

 

Не особая матрица со столбцами обеспечивающая представление матрицы динамики в форме Калмана строится рекуррентно по следующим формулам:

 

Рассмотрим систему с регулятором.

 

- корни уравнения

;

;

.

 

Какова связь между и ?

 

;

 

 

Результат показывает, что матрица динамики системы с обратной связью тоже в форме Калмана, а следовательно в последней строке этой матрицы находятся коэффициенты нового характеристического уравнения , которые связаны со старыми следующим образом:

;

 

– коэффициенты характеристического уравнения матрицы динамики с обратной связью;

; ;

 

Путем выбора значений можно получить желаемое значение коэффициентов характеристического уравнения матрицы динамики , что соответствует желаемым значениям коэффициентов характеристических чисел, отсюда:

.