Второй закон термодинамики определяет направление протекания процесса.
Для обратимых процессов отношение:
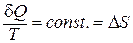 ;
;
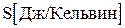 – функция состояния системы, названная энтропией, равна:
– функция состояния системы, названная энтропией, равна:
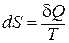 ,
,
Второй закон термодинамики в дифференциальной форме:
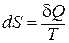
 , так как в изолированной системе:
, так как в изолированной системе:  .
.
Энтропия имеет вероятностную природу:
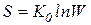 ,
,
где 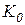 - постоянная Больцмана,
- постоянная Больцмана, 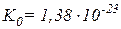 Дж К-1,
Дж К-1,
а 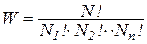 ,
,
причем 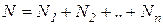 - число вероятных состояний системы.
- число вероятных состояний системы.
Таким образом, I-й закон ТД определяет энергетический баланс в закрытой системе, а II-й – дает возможность установить направленность термодинамического процесса.
Термодинамические потенциалы
По изменению 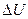 и
и 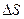 нельзя оценить величину производимой работы, их начальных и конечных значений. Для этого и вводят термодинамические потенциалы, которые выводятся из объединенной записи I-го и II-го законов термодинамики.
нельзя оценить величину производимой работы, их начальных и конечных значений. Для этого и вводят термодинамические потенциалы, которые выводятся из объединенной записи I-го и II-го законов термодинамики.
Объединённая запись I и II законов ТД.
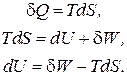
Видно, что изменение внутренней энергии складывается из двух компонентов:
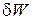 - совершаемая работа – это свободная энергия,
- совершаемая работа – это свободная энергия,
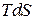 – рассеянная в виде тепла – связанная энергия.
– рассеянная в виде тепла – связанная энергия.
Для количественной оценки свободной энергии необходимо наложить ограничения:
1. При постоянном давлении P, работа по изменению объёма будет равна 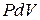 , а количество теплоты, согласно I-му закону ТД:
, а количество теплоты, согласно I-му закону ТД:
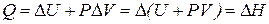
будет отражать изменение энтальпии – теплосодержание системы.
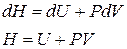
Т.е. энтальпия равна количеству теплоты, выделяемой системой.
Зная энтальпию исходных веществ и продуктов реакции и основываясь на законе Гесса, можно определить её тепловой эффект (см. стр.12)
2. При постоянных V и T рассчитывается свободная энергия Гельмгольца.
Совершаемая работа условно состоит из 2-х компонент:

так как 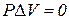 ,
,
 - свободная энергия Гельмгольца.
- свободная энергия Гельмгольца.
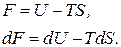
3. При постоянных P и T рассчитывается свободная энергия Гиббса:
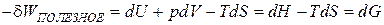 –свободная энергия Гиббса, и она равна:
–свободная энергия Гиббса, и она равна:
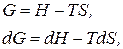
Так как в биологических системах 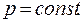 , чаще используют энергию Гиббса.
, чаще используют энергию Гиббса.
Следствия I и II –го законов ТД.
1. Необратимый процесс всегда сопровождается рассеянием энергии в тепло 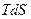 ;
;
2. Если 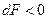 или
или 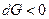 , то процесс самопроизвольный и необратим, если
, то процесс самопроизвольный и необратим, если  и
и 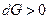 , то процесс не самопроизвольный и обратимый.
, то процесс не самопроизвольный и обратимый.
3. При достижении равновесия 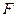 и
и  , а
, а 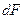 и
и 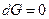
Закон Вант – Гоффа
Для идеального газа с учетом того, что свободная энергия Гиббса при полном дифференциировании: dG = dU + pdV + VdP – TdS – SdT = VdP-SdT, где:
dG = VdP-SdT
и постоянной температуре, получим:

Если первое состояние – в стандартных условиях и имеет стандартную величину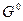 , то итоговое значение свободной энергии Гиббса будет равно:
, то итоговое значение свободной энергии Гиббса будет равно:
 .
.
Для разбавленных растворов 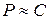 (концентрация) и тогда:
(концентрация) и тогда: 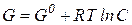 .
.
Для простого процесса 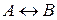 в состоянии равновесия
в состоянии равновесия 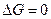 , тогда,
, тогда,
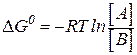
а так как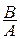 =
=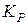 (константа равновесия), получаем:
(константа равновесия), получаем:
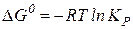 – закон Вант – Гоффа
– закон Вант – Гоффа
(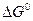 - изменение
- изменение 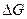 при протекании процесса в стандартных условиях).
при протекании процесса в стандартных условиях).
В биологических системах процессы обычно сопровождаются еще изменением количества вещества и в таком случае:
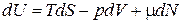 ,
,
где 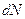 - изменение числа частиц,
- изменение числа частиц,
 - химический потенциал (градиент).
- химический потенциал (градиент).
 .
.
Химический потенциал равен изменению термодинамического потенциала, приходящегося на одну частицу вещества в соответствующем процессе. Он не является термодинамическим потенциалом и служит параметром системы.
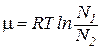
Все выше изложенное разработано для закрытых и изолированных систем, находящихся в состоянии термодинамического равновесия. При этом состоянии, когда: 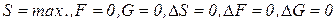 , процессы не протекают, материя мертва, так как система не может самопроизвольно выйти из этого состояния.
, процессы не протекают, материя мертва, так как система не может самопроизвольно выйти из этого состояния.
Живые системы находятся в стационарном состоянии. При этом скорость протекания процессов остается постоянной, то есть: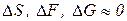 , но
, но 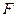 и
и 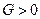 , а
, а 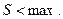 (здесь
(здесь 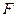 и
и  становятся функциями от времени).
становятся функциями от времени).
Равновесие в живой системе поддерживается за счет баланса протекающих процессов.