ЛЕКЦИЯ 8 Нормальный закон и его параметры
2. Моменты нормального распределения.
3. Вероятность попадания нормально распределенной величины на заданный интервал.
2.1.2. Нормальный закон распределения а) Нормальный закон и его параметры.
Главная особенность, выделяющая нормальный закон среди других состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при часто вращающихся типичных условиях. Большинство встречающихся на практике случайных величин, таких, например, как ошибки измерений могут быть представлены как суммы большого числа сравнительно малых слагаемых – элементарных ошибок, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные ошибки, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, накладываемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль.
Нормальное распределение является наиболее изученным распределением. Поэтому его стараются использовать и при изучении случайных величин, распределения которых отличны от нормального. Здесь могут быть два основных пути.
Первый путь заключается в переходе по определенной формуле, которую вследствие можно будет учесть, от заданной величины к другой, имеющей нормальное распределение. Например, при изучении случайной величины X может оказаться, что нормальное распределение имеет ее логарифм, т.е.  . Тогда вместо X следует рассматривать случайную величину
. Тогда вместо X следует рассматривать случайную величину  , пересчитав все исходные данные применительно к ней Получив с помощью формул нормального распределения все неободимые результаты для Y, следует вновь вернуться к исходной случайной величине X. Второй путь заключается в приближенной замене распределения исследуемой случайной величины нормальным. Он особенно часто применяется при .обработке экспериментальных данных, где, как правило, нет возможности установить распределение случайной величины с абсолютной точностью.
, пересчитав все исходные данные применительно к ней Получив с помощью формул нормального распределения все неободимые результаты для Y, следует вновь вернуться к исходной случайной величине X. Второй путь заключается в приближенной замене распределения исследуемой случайной величины нормальным. Он особенно часто применяется при .обработке экспериментальных данных, где, как правило, нет возможности установить распределение случайной величины с абсолютной точностью.
Нормальный закон распределения характеризуется плотностью вероятности, определяемой зависимостью вида:
 . (2.14)
. (2.14)
Кривая распределения, соответствующая нормальному закону имеет симметричный холмообразный вид (рис. 2.10). Максимальная ордината кривой равна  и соответствует точке
и соответствует точке  . По мере удаления от точки m плотность распределения падает и при
. По мере удаления от точки m плотность распределения падает и при  кривая асимптотически приближается к оси абсцисс.
кривая асимптотически приближается к оси абсцисс.

Рис. 2.10
Параметры распределения m и s имеют совершенно определенный смысл: m – математическое ожидание, а s – среднее квадратичеекое отклонение величины распределенной по нормальному закону. Покажем это. В соответствии с определением:
 .
.
Осуществляя замену переменной  , получим:
, получим:
 .
.
Поскольку первая подинтегральная функция нечетная, а вторая – четная, то при симметричных пределах интегрирования первый интеграл равен нулю, а второй:
 .
.
Таким образом:  .
.
По определению:
 .
.
После замены переменной  , имеем:
, имеем:
 .
.
Интегрируя по частям, и полагая:  ,
,  , а
, а  ;
;  будем иметь:
будем иметь:
 .
.
Следовательно:  .
.
Из (2.14) следует, что кривая распределения имеет ось симметрии, проходящую через точку с абсциссой m . Т.е. математическое ожидание характеризует положение кривой распределения на оси абсцисс и при его изменении кривая соответствующим образом сдвигается (рис. 2.11).

Рис. 2.11
Параметр s характеризует не положение, а форму кривой распределения: наибольшая ордината кривой распределения обратно пропорциональна s. Так как площадь под кривей распределения всегда равна единице, то с увеличением s кривая становится более плоской, растягиваясь вдоль оси абсцисс и наоборот (рис 2.12).

Рис. 2.12.
б) Моменты нормального распределения.
Получим зависимости для вычисления моментов высоких порядков, в частности третьего и четвертого.
По определению:
 .
.
После известной замены переменной и интегрирования по частям, получается относительно простое рекуррентное соотношение для вычисления центральных моментов высокого порядка через моменты более низких:
 . (2.15)
. (2.15)
Имея в виду, что  (
( ), а
), а  (
( ), из (2.15) следует, что все нечетные центральные моменты любого порядка, в том числе и
), из (2.15) следует, что все нечетные центральные моменты любого порядка, в том числе и  равны 0. Откуда
равны 0. Откуда  , т.е. асимметрия распределения нормального закона равна 0. Для четных моментов справедливы следующие уравнения:
, т.е. асимметрия распределения нормального закона равна 0. Для четных моментов справедливы следующие уравнения:  ;
;  ;
;  и т.д. Откуда следует выражение для эксцесса:
и т.д. Откуда следует выражение для эксцесса:
 .
.
в) Вероятность попадания нормально распределенной величины на заданный интервал.
Наиболее распространенной задачей, связанной с нормально распределенными случайными величинами, является определение вероятности попадания такой величины на участок 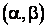 . По определению эта вероятность равна:
. По определению эта вероятность равна:
 .
.
Так как Х распределена по нормальному закону с плотностью  , то
, то  .
.
После известной замены  интеграл приводится к виду:
интеграл приводится к виду:
 .
.
Полученный интеграл не выражается через элементарные функции, но его можно выразить через специальные функции, значения которых заранее вычислены и сведены в таблицы.
Наиболее распространенной специальной функцией, используемой для этого, является функция вида:
 . (*)
. (*)
Функция (*) совпадает с функцией распределения для нормально распределенной случайной величины с параметрами  ,
,  .Функцию распределения
.Функцию распределения  можно выразить через функцию (*):
можно выразить через функцию (*):
 . (2.16)
. (2.16)
Откуда:
 . (2.17)
. (2.17)
Аргументы функции  в (2.17) имеют определенный физический смысл: это расстояния от концов интервала до математического ожидания (центра рассеивания), выраженное в средних квадратических отклонениях.
в (2.17) имеют определенный физический смысл: это расстояния от концов интервала до математического ожидания (центра рассеивания), выраженное в средних квадратических отклонениях.
Функция  в соответствии с (2.16) может рассматриваться как функция распределения, а следовательно она обладает известными свойствами:
в соответствии с (2.16) может рассматриваться как функция распределения, а следовательно она обладает известными свойствами:
1.  ;
;
2.  ;
;
3.  – неубывающая функция.
– неубывающая функция.
Кроме того:
 , (2.18)
, (2.18)
что следует из симметричности  относительно точки с координатами
относительно точки с координатами  – рис. 2.13.
– рис. 2.13.

Рис. 2.13
Пользуясь свойством (2.18) таблицы функций  можно ограничить лишь положительными значениями аргумента.
можно ограничить лишь положительными значениями аргумента.
Очень часто интервал 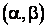 оказывается симметричным относительно математического ожидания m случайной величины X Вероятность попадания X на этот участок длиной 2l в соответствии с формулой (2.17) определится:
оказывается симметричным относительно математического ожидания m случайной величины X Вероятность попадания X на этот участок длиной 2l в соответствии с формулой (2.17) определится:  . Но по (2.18) имеем:
. Но по (2.18) имеем:  . Тогда
. Тогда  или:
или:
 (2.19)
(2.19)
Из (2.19) следует: вероятность того, что абсолютное отклонение нормально распределенной величины от ее математического ожидания не превзойдет некоторого предела, зависит только от того. во сколько этот предел больше стандарта рассматриваемой величины.
При  .
.
При  .
.
При  .
.
Если брать приближенные значения вероятностей, то получаются удобные для запоминания правила:
1. Правило s. Вероятность стандартного отклонения равна  или 66 %.
или 66 %.
2. Правило 2s. Вероятность удвоенного стандарта равна 95 %.
3. Правило Зs . Вероятность утроенного стандарта равна 1, т.е. отклонения больше, чем утроенный стандарт, практически невозможны.